Informatik II - Übung 1 (Spoilerfree)

Pascal Schärli

info2@pascscha.ch

25.09.2020

Administratives

Pascal Schärli 25.09.2020

Code Expert

  • Code Expert bleibt gleich wie in Info I
     
  • Wenn Ihr die Aufgaben gut genug löst, bekommt ihr XP.
     
  • Mit XP kann man Bonusübungen freischalten, welche bis zu ¼ Note Bonus auf die Prüfung geben.
     
  • Textaufgaben könnt ihr mit Markdown schön formatieren.

Pascal Schärli 25.09.2020

Code Expert - Files hochladen

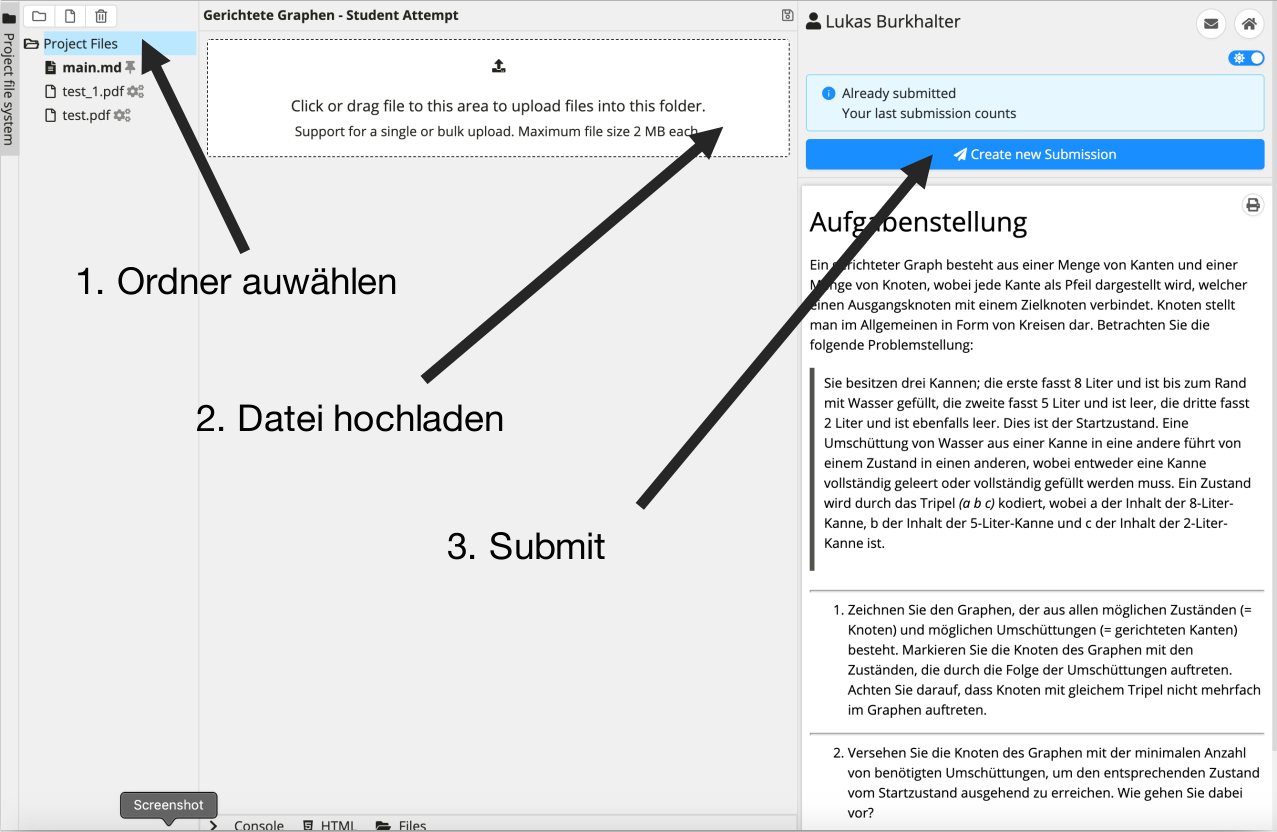
Pascal Schärli 25.09.2020

Eclipse

  • Da der Text Editor in CodeExpert noch nicht gleich mächtig ist wie eine IDE, benutzen wir Eclipse fürs Programmieren.
     
  • Eclipse könnt ihr hier gratis herunterladen: https://www.eclipse.org/downloads/
     
  • Workflow:
    1. Ladet euch das .zip File der Übung von der Vorlesungsseite herunter
    2. Löst die Übung in Eclipse
    3. Kopiert euer Code zu CodeExpert

Pascal Schärli 25.09.2020

Eclipse

Wie man das .zip File in Eclipse öffnet

Pascal Schärli 25.09.2020

JUnit

Wie man automatische Tests mit JUnit macht

Pascal Schärli 25.09.2020

Eclipse Shortcuts

Pascal Schärli 25.09.2020

  • Ctrl+Shift+F

Code Formattieren

  • Ctrl+Space

Autocomplete

  • Ctrl+D

Zeile Löschen

  • Ctrl+Shift+7

markierte Zeilen als Kommentar

  • Ctrl+F11

Programm ausführen

  • Ctrl+Shift+L

Liste aller Shortcuts anzeigen

Eclipse Shortcuts

Pascal Schärli 25.09.2020

  • Ctrl+Shift+F

Code Formattieren

  • Ctrl+Space

Autocomplete

  • Ctrl+D

Zeile Löschen

  • Ctrl+Shift+7

markierte Zeilen als Kommentar

  • Ctrl+F11

Programm ausführen

  • Ctrl+Shift+L

Liste aller Shortcuts anzeigen

Nachbesprechung

Pascal Schärli 25.09.2020

Serie 0 - Hello World

  1. Java Development Kit (JDK) Version 13 herunterladen:
  2. HelloWorld.java in Konsole ausführen
     
  3. Programm in Eclipse ausführen
     
  4. Programm in CodeExpert rüberkopieren und einreichen

Pascal Schärli 25.09.2020

Serie 0 - Signum

  1. Programm kann mit dem grünen Knopf ausgeführt werden
     
  2. Fügt in Main.java eine weitere Zeile ein, z.B.:

     
  3. Programm in CodeExpert rüberkopieren und einreichen

Pascal Schärli 25.09.2020

System.out.println("signum(3) = " + Signum.signum(3));

Serie 0 - JUnit

  1. Im Video vorher habe ich gezeigt wie ihr JUnit einbinden könnt.
     


  2.  
  3. Programm in CodeExpert rüberkopieren und einreichen
@Test public void positive2() {
    Assert.assertEquals(1, Signum.signum(10));
}

Pascal Schärli 25.09.2020

Serie 0 - Graphen

Zeichnen Sie den Graphen, der aus allen möglichen Zuständen und Umschüttungen besteht.

\frac{\sum{f(x) * x}}{\sum{f(x)}} = \frac{1 * 2 + 2 * 3 + 3 * 2 + 4 * 2 + 5 * 2 + 6 * 2}{2+3+2+2+2+2}
= \frac{44}{13} \approx 3.38

Pascal Schärli 25.09.2020

Vorlesung

Pascal Schärli 25.09.2020

f(a,b) = \begin{cases} a &, \text{falls } b = 1\\ f(2a,b/2) &, \text{falls b gerade}\\ f(2a,\frac{b-1}{2}) + a &, \text{sonst} \end{cases}

Altägyptische Multiplikation

(Russische Bauernmultiplikation / Russian Peasant Multiplication)

f(a,b) = a \cdot b

Pascal Schärli 25.09.2020

f(a,b) = \begin{cases} a &, \text{falls } b = 1\\ f(2a,b/2) &, \text{falls b gerade}\\ f(2a,\frac{b-1}{2}) + a &, \text{sonst} \end{cases}

Altägyptische Multiplikation

(Russische Bauernmultiplikation / Russian Peasant Multiplication)

a b f(a,b) 
f(5,98)   = f(10,49)

f(10,49)  = f(20,24) + 10

f(20,24)  = f(40,12)

f(40,12)  = f(80,6)

f(80,6)   = f(160,3)

f(160,3)  = f(320,1) + 160

f(320,1)  = 320

f(5,98) = 320 + 160 + 10 = 490

5

10

20

40

80

160

320

98

49

24

12

6

3

1

Pascal Schärli 25.09.2020

Altägyptische Multiplikation

Induktiver Beweis über \(b\) (Slides 207)

Induktionsverankerung: \(b = 1 \)

f(a,1) = a = a \cdot 1

Induktionsschritt:

Gegeben, dass \(f(a,b) = a \cdot b \) für \(b \in [1 \dots n-1] \).

Zeige daraus, dass \(f(a,n) = a \cdot n\).

\(n\) gerade:

\(f(a,n) = f(2a,\frac{n}{2})\)

\(=2a \cdot \frac{n}{2}\)

\(=a \cdot n \)

\(n\) ungerade:

\(f(a,n) = f(2a,\frac{n-1}{2}) + a\)

\(=2a \cdot \frac{n-1}{2} + a\)

\(=a \cdot (n-1) + a \)

\(=a \cdot n \)

f(a,b) = \begin{cases} a &, \text{falls } b = 1\\ f(2a,b/2) &, \text{falls b gerade}\\ f(2a,\frac{b-1}{2}) + a &, \text{sonst} \end{cases}

Pascal Schärli 25.09.2020

Laufzeitkomplexität

static int summe(int x) {
    if (x == 0) return 0;
    return summe(x-1) + x;
}
summe(5) = summe(4) + 5
summe(4) = summe(3) + 4
summe(3) = summe(2) + 3
summe(2) = summe(1) + 2
summe(1) = summe(0) + 1
summe(0) = 0
= 10 + 5 = 15

= 6 + 4 = 10
= 3 + 3 = 6
= 1 + 2 = 3
= 0 + 1 = 1
= 0

-> \(summe(x)\) ruft sich selbst \(x\) mal rekursiv auf

Beispiel

1

2

3

4

5

Pascal Schärli 25.09.2020

Exceptions

public static void pleaseDontPassZero(int i) throws IllegalArgumentException {
    if(i == 0){
        throw new IllegalArgumentException("I told you so!");
    }
}

Pascal Schärli 25.09.2020

Achtung, diese Funktion könnte einen Fehler werfen

"Werfe" einen neuen Fehler

public static void foo1() throws IllegalArgumentException {
	pleaseDontPassZero(1);
}

public static void foo2() {
    try{
        foo1();
    } 
    catch(IllegalArgumentException e){
    	System.out.println("Something went wrong.");
    }
}

Fehler müssen weitergeleitet oder gefangen werden:

Pascal Schärli 25.09.2020

Vorbesprechung

Pascal Schärli 25.09.2020

Altägyptische Multiplikation

(Russische Bauernmultiplikation / Russian Peasant Multiplication)

  1. Wäre der Beweis (siehe BestOf) auch mit Induktion über a möglich?
     
  2. Beweist, dass der Algorithmus für alle erlaubten Eingabewerte terminiert
     
  3.  
     
static int f(int a, int b){
  System.out.println(a + " " + b);
  if (b == 0)
  	return 0;
  else if (b%2 == 0)
  	return f(a+a, b/2);
  else
  	return a + f(a+a, (b-1)/2);
}
static int f(int a, int b){
  System.out.println(a + " " + b);
  if (b == 1)
  	return a;
  else if (b%2 == 0)
  	return f(a+a, b/2);
  else
  	return a + f(a+a, (b-1)/2);
}

Pascal Schärli 25.09.2020

Laufzeitkomplexität

static boolean gerade(int x) {
    if (x == 0) return true;
    return !gerade(x-1);
}

static int verdopple(int x) {
    if ( x == 0 ) return 0;
    return 2 + verdopple(x-1);
}

static int halbiere(int x) {
    if (x == 0) return 0;
    if (x == 1) return 0;
    return 1 + halbiere(x-2);
}

static int f(int a, int b) {
    if (b == 0) return 0;
    if (gerade(b))
    	return f(verdopple(a), halbiere(b));
    else
    	return a + f(verdopple(a), halbiere(b));
}
  1. Wie oft rufen sich die Funktionen auf bevor sie terminieren?
     
  2. Wie viele Funktionen werden bei f(a,b) vor der return-Zeile aufgerufen?
     
  3. Wie viele Funktionen werden bei f(a,b) inklusive return-Zeile aufgerufen?

Pascal Schärli 25.09.2020

Überprüfung Benuzereingaben

  • Teilaufgabe a)

    • Implementation der Altägyptische Multiplikation gegeben, nur positive Zahlen erlaubt!

    • Nicht erlaubte Eingaben müssen einen Fehler (Exception) auslösen 

  • Teilaufgabe b)

    • Findet den Fehler in der Funktion f

Pascal Schärli 25.09.2020

private static int f(int a, int b) {
    if (b==0) return a;
    if (b%2 == 0) return f(2*a, b/2);
    else return a + f(2*a, b/2);
}

Überprüfung Benuzereingaben

  • Java Doc: Standard für Java Dokumentationen (Kommentarte)
  • Vor jeder Funktion:






     
  • In Eclipse: /** + Enter

c) - Java Doc

/**
* Beschreibung
*
* @param a 	Beschreibung Variable a
* @param b 	Beschreibung Variable b
* @return 	Beschreibung Rückgabewert
* @throws 	Beschreibung Exceptions
*/

Pascal Schärli 25.09.2020

Viel Spass!

Pascal Schärli 25.09.2020