Informatik II - Übung 10

Nachbesprechung

Pascal Schärli 27.11.2020
Pascal Schärli 27.11.2020
Pascal Schärli 27.11.2020
Pascal Schärli 27.11.2020
Vorlesung

Pascal Schärli 27.11.2020
Divide and conquer
- Komplexe Probleme können auf einfache Teilprobleme reduziert werden
- Diese Teilprobleme kann man weiter unterteilen, bis das Problem simpel genug ist
-
Teile und Herrsche
- Heute:
- Türme von Hanoi
- Mergesort
Pascal Schärli 27.11.2020
Türme von Hanoi
Turm 1
Turm 2
Turm 3


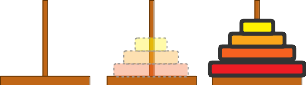
- Das Ziel ist es, alle Scheiben von Turm 1 nach Turm 3 zu verschieben.
- Man darf immer nur eine Scheibe auf einmal verschieben
- Es darf nie eine grössere Scheibe auf einer kleineren liegen.
Pascal Schärli 27.11.2020
- Wir wollen \(n\) Scheiben von Turm 1 nach Turm 3 verschieben:
- \(n-1\) Scheiben von Turm 1 nach Turm 2 verschieben
- Grosse Scheibe von Turm 1 nach Turm 3 verschieben
- \(n-1\) Scheiben von Turm 2 nach Turm 3 verschieben
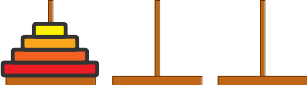
\(n = 4\)
Turm 1
Turm 3
Turm 2





[1]
[2]
[3]
[4]
Türme von Hanoi
Pascal Schärli 27.11.2020

\(n = 4\)
Turm 1
Turm 3
Turm 2






[1]
[2]
[3]
[4]
- Im Zug 2 und 4 verschieben wir mehr als eine Scheibe
- Wir müssen einen Weg finden die \(n - 1\) Scheiben zu verschieben ohne die Regeln zu verletzen
- Wir verwenden unseren divide and conquer Algorithmus für die \(n - 1\) Scheiben
Türme von Hanoi
Pascal Schärli 27.11.2020
- Wir wollen \(n-1\) Scheiben von Turm 1 nach Turm 2 verschieben:
- \(n-2\) Scheiben von Turm 1 nach Turm 3 verschieben
- Eine Scheibe von Turm 1 nach Turm 2 verschieben
- \(n-2\) Scheiben von Turm 3 nach Turm 2 verschieben

\(n = 4\)
Turm 1
Turm 3
Turm 2


[1]
[2]
[3]
[4]




Türme von Hanoi
Pascal Schärli 27.11.2020

\(n = 4\)
Turm 1
Turm 3
Turm 2






[1]
[2]
[3]
[4]
Dies können wir in einem Rekursiven Algorithmus festhalten:
hanoi(int n, int von, int nach){
if(n == 1) movetop(von,nach);
int other = 6 - von - nach;
hanoi(n-1,von,other); // [2]
movetop(von,nach); // [3]
hanoi(n-1,other,nach); // [4]
}Türme von Hanoi
Pascal Schärli 27.11.2020
Mergesort
Mergesort ist ein Sortieralgorithmus, welcher ebenfalls durch divide and conquer funktioniert
- Teile die Liste in zwei halb so grosse Listen auf
- Sortiere die halb so grossen Listen
- Verbinde die beiden sortierten Listen zu einer einzigen sortierten Liste
3
8
6
5
2
7
4
1
1
2
3
4
5
6
7
8
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
1
2
3
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
1
2
3
4
5
6
7
8
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
1
2
3
- Im Punkt 2 können wir die kleinen Teillisten wieder mit Mergesort sortieren
- Dies wiederholen wir, bis die Liste nur noch ein Element beinhaltet

Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Mergesort
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Pascal Schärli 27.11.2020
Laufzeitkomplexität
- Beschreibt Anzahl Rechenschritte die ein Algorithmus für das Lösen in Abhängigkeit von der Inputgrösse \(n\) braucht
- Wir betrachten die asymptotische Laufzeit, also nicht wie gross der Zeitaufwand ist, sondern wie schnell er im Verhältnis zur Inputgrösse wächst.
- Diese Abschätzungen machen wir mit der Landau-Notation (Big O notation)
- Wir betrachten nur den am schnellsten Wachsenden Summanden und ignorieren alle konstanten Faktoren
Pascal Schärli 27.11.2020
Laufzeitkomplexität
\(\frac{1}{2^{n!}} + 10 + n^2 + 3*n^5\)
\(O(n^5)\)
\(\frac{1}{7}(n! + 2^n + n^2)\)
\(O(n!)\)
\(log(n) + n*log_3(n)\)
\(O(n*log(n))\)
\(2^{n + 5}\)
\(O(2^n)\)
\(\frac{n}{n + 5}\)
\(O(1)\)
Pascal Schärli 27.11.2020
Laufzeitkomplexität Mergesort
\(T(n) \approx 2^1 \cdot T(\frac{n}{2^1}) + n\)
\(T(n) \approx 2^1 \cdot (2 \cdot T(\frac{n}{2^2}) + \frac{n}{2}) + n\)
\(T(n) \approx 2^2 \cdot T(\frac{n}{2^2}) + 2 \cdot n\)
\(T(n) \approx 2^3 \cdot T(\frac{n}{2^3}) + 3 \cdot n\)
\(T(n) \approx 2^4 \cdot T(\frac{n}{2^4}) + 4 \cdot n\)
\(\cdots\)
\(T(n) \approx 2^{log_2(n)} \cdot T(1) + log_2(n) \cdot n\)
\(T(n) \approx n \cdot T(1) + log_2(n) \cdot n\)
\(\Rightarrow\) Laufzeitkomplexität von Mergesort: \(O(n \cdot log(n))\)
Pascal Schärli 27.11.2020

Pascal Schärli 27.11.2020
Vorbesprechung

Pascal Schärli 27.11.2020
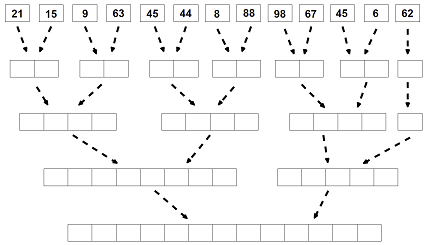
- Führt Mergesort von Hand aus
- Plottet die Messungen von Aufgabe 3 mit einem log-log plot
Pascal Schärli 27.11.2020
-
Erstellt eine Hilfsfunktion, welche den Array in einem Bestimmten Intervall [begin, end) sortiert
-
Macht Messungen um zu schauen ob die Ausführungszeit wirklich Logarithmisch steigt
public static void main(String[] args) {
int counts[] = {100, 200, 400, 800, 1600, 3200, 6400, 12800, 25600, 51200, 102400};
for (int count : counts) {
double result = measure(count);
System.out.println(String.format("%d: %.2f ms", count, result));
}
}Pascal Schärli 27.11.2020
#!/usr/bin/python3
from matplotlib import pyplot as plt
import random
if __name__ == "__main__":
counts = [100, 200, 400, 800, 1600, 3200, 6400, 12800, 25600, 51200]
# TODO: Replace line below with your measurements:
times = [random.random()*c for c in counts]
# Set title and axis labels
plt.title("Mergesort Time measurements")
plt.xlabel("Input size")
plt.ylabel("Time [s]")
# Set axis scale to log-log plot
plt.xscale("log")
plt.yscale("log")
# Plot our data on the plot
plt.plot(counts, times, color="black")
# Save an image of the plot to plot.png
plt.savefig("plot.png")
# Show the resulting plot
plt.show()
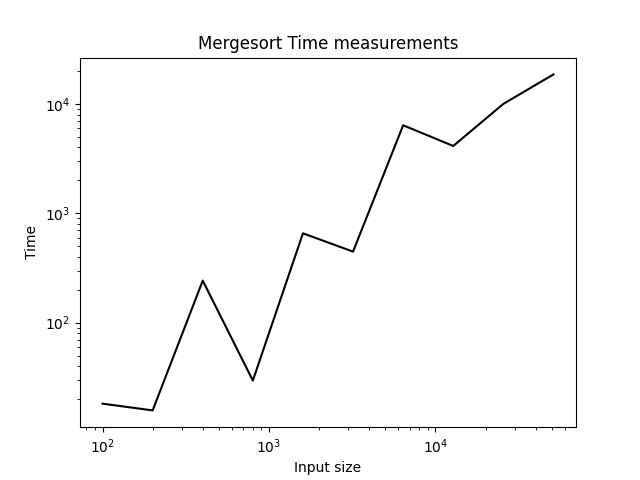
Tipp: Die coolen Kids heutzutage benutzen Python mit Matplotlib
(not sponsored)
Pascal Schärli 27.11.2020

- Bestimmt für jeden Schritt welche Türme jeweils nicht verwendet werden um alle Scheiben von Turm 1 nach Turm 3 zu verschieben
- Erstellt einen Iterativen Algorithmus um das Problem zu lösen
- Funktioniert der Iterative Algorithmus auch bei Höhe 5?
Pascal Schärli 27.11.2020
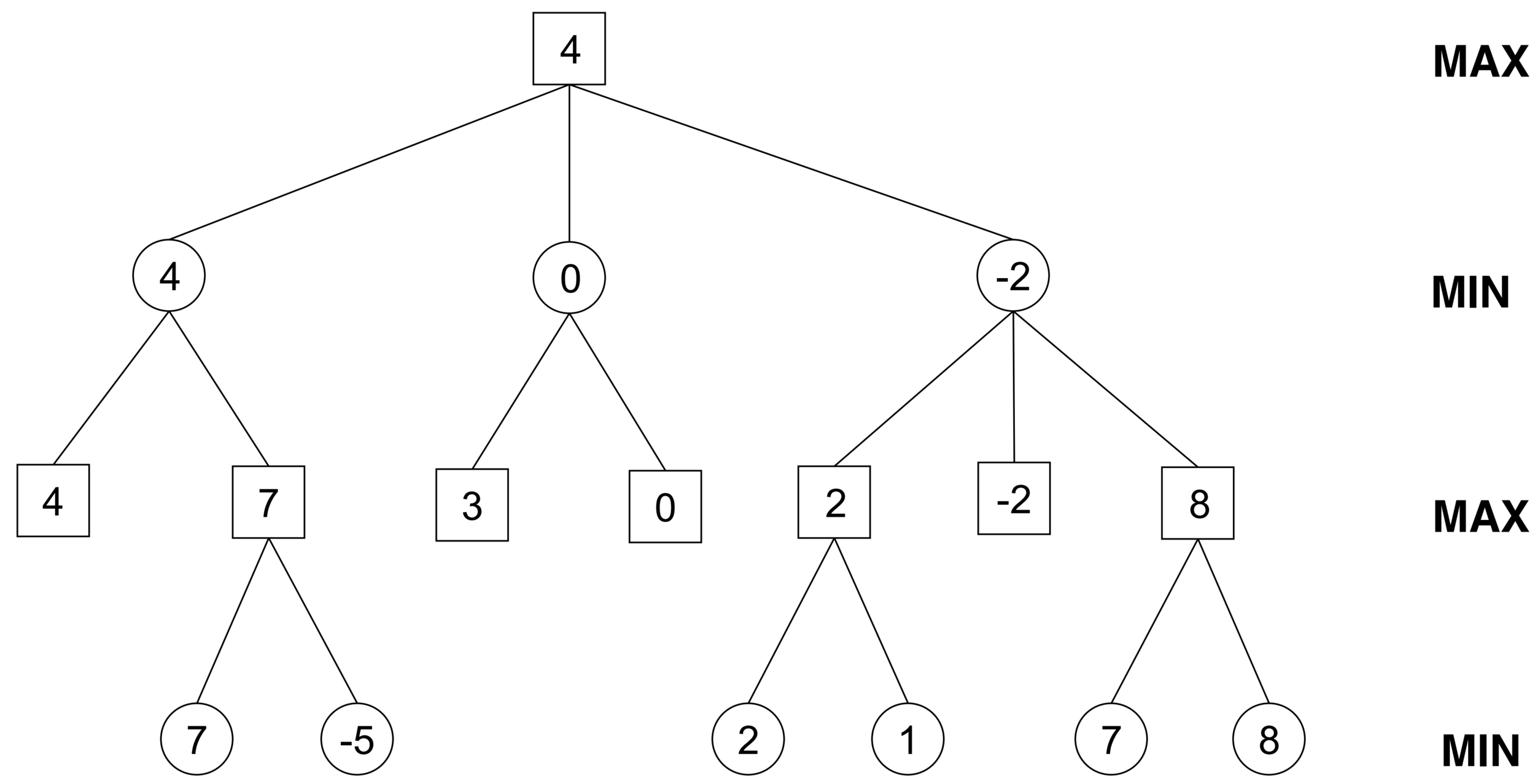
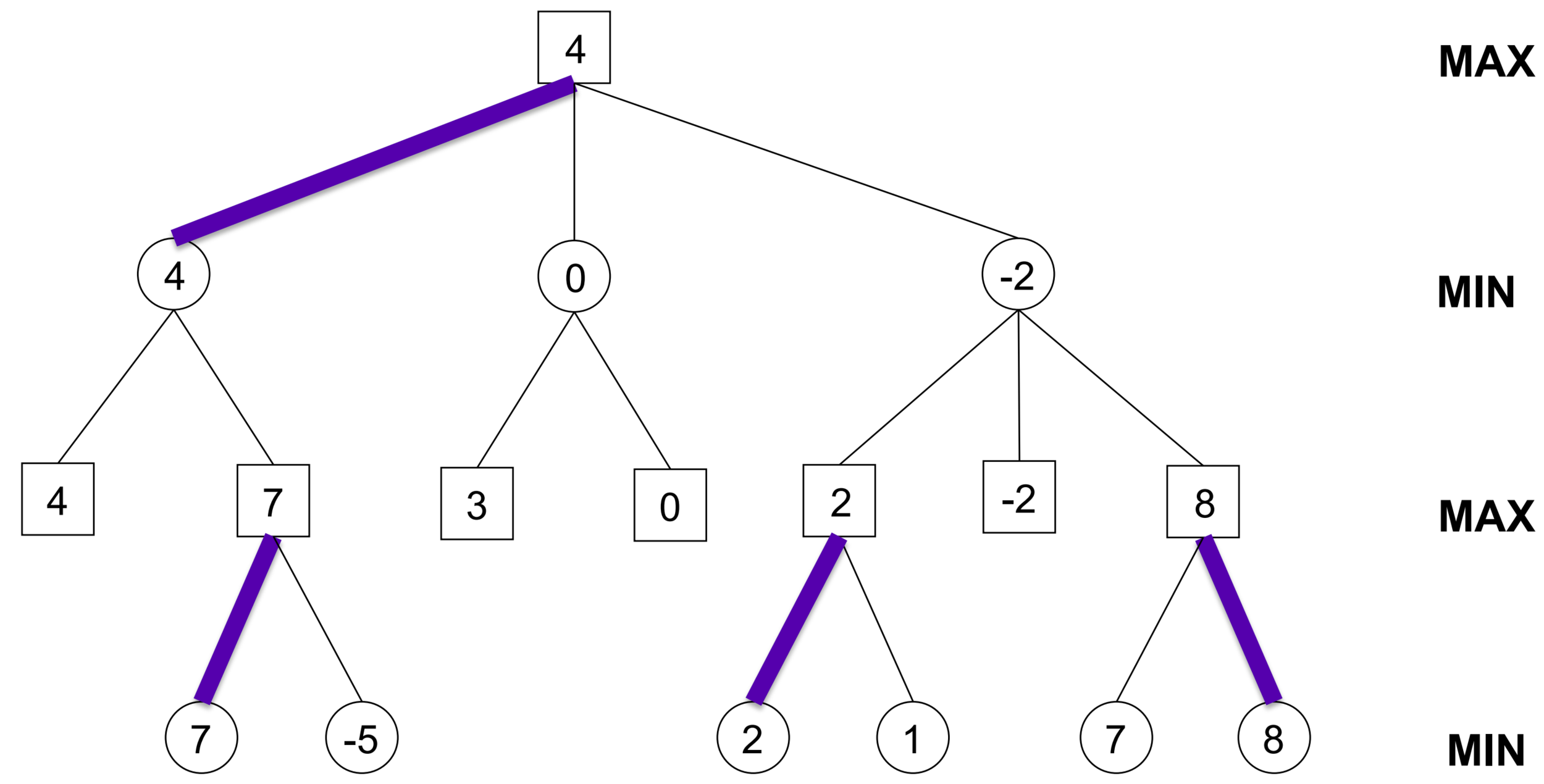
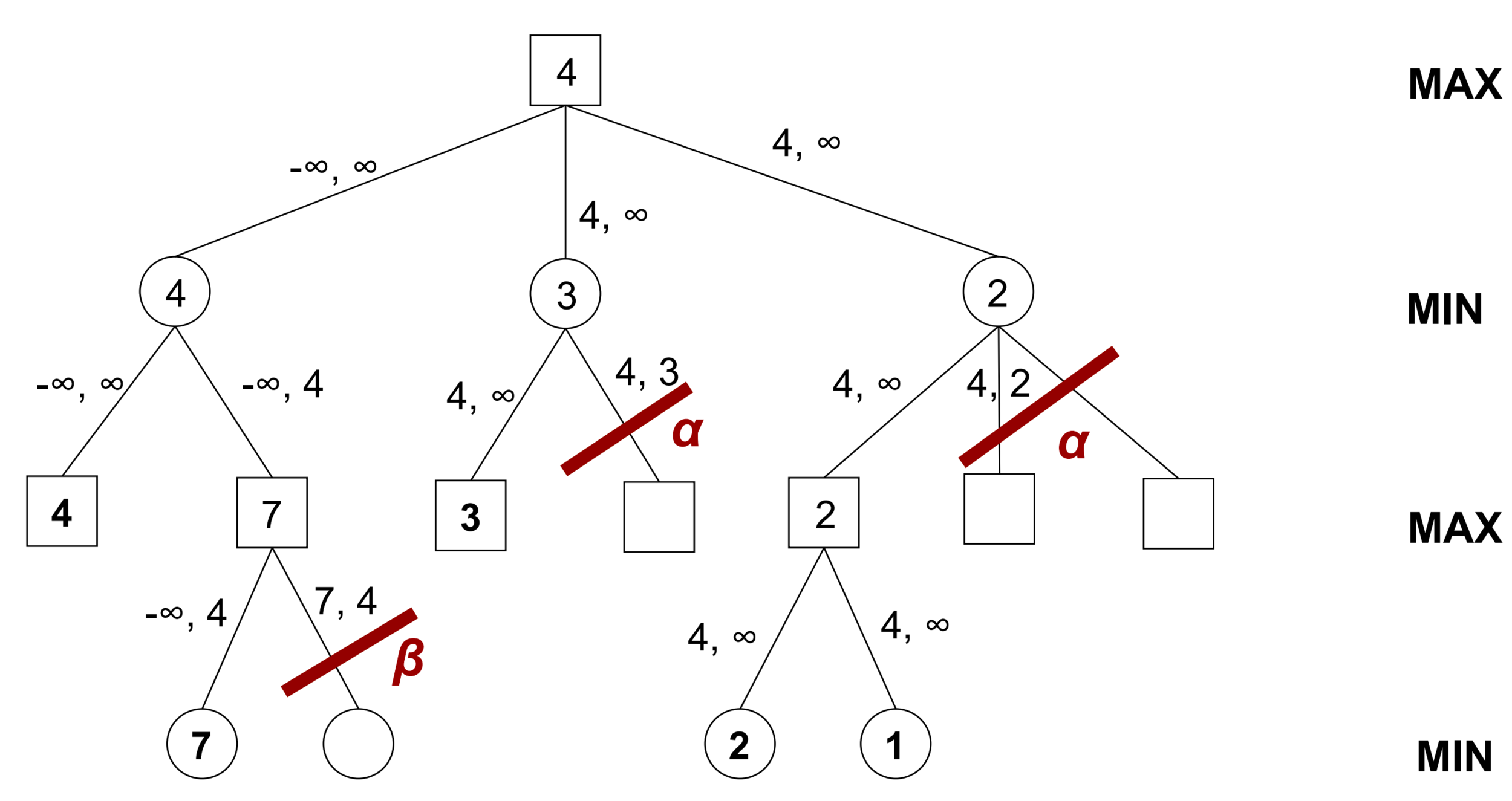
- Implementiert Alpha/Beta Algorithmus
- Verwendet euren MiniMax Spieler von letzter Woche oder die Musterlösung als Vorlage
- Gebt zusätzlich noch alpha / beta Parameter mit, um eure Cuts zu machen.
- Versucht weiter eure Feldbewertung zu verbessern
Pascal Schärli 27.11.2020
Viel Spass!

Pascal Schärli 27.11.2020
