Informatik II - Ãœbung 3

Pascal Schärli

IloveExercise3@pascscha.ch

09.10.2020

Nachbesprechung

Bild: look again by corpus delicti from the Noun Project

Pascal Schärli 09.10.2020

Sortieren

public String toString() {
    String s="[";
    for (int i=0; i<numbers.length; i++) {
        if (i!=0) {
            s = s + ", ";
        }
        s = s + numbers[i];
    }
    s = s + "]";
    return s;
}

Pascal Schärli 09.10.2020

Sortieren

private void recursiveSort(int until) {
    if (until == 0) {
        return;
    } else {
        recursiveSort(until - 1);
            
        int index_max = until-1;
        for (int i=until; i<numbers.length; i++) {
           if (numbers[i] > numbers[index_max]) {
                index_max = i;
            }
        }
        swap(until - 1, index_max);
    }
}

Pascal Schärli 09.10.2020

Binärbäume als Arrays

  private static void checkTree(char[] array) throws IllegalArgumentException
  {
    if(array.length==0)
      throw new IllegalArgumentException("empty tree");
    for(int i=0;i<array.length;i++) {
      if((array[i]!=' ')&&(array[father(i)]==' '))
        throw new IllegalArgumentException("empty father");
    }
  }

Pascal Schärli 09.10.2020

Binärbäume als Arrays

private String toString(int node, String indentation){
  String res="";
  if(tree[node]==' ')
    return "";
    
  // add the first one to the node
  res=indentation+Character.toString(tree[node])+"\n";
  
  //Check if the child node is still inside
  if(leftChild(node)<tree.length&&leftChild(node)!=' ') {    
      res=res+toString(leftChild(node),indentation+" ");
    }
    
    //also check if there is a right child  
    if((rightChild(node)<tree.length)&&(rightChild(node)!=' ')) {
      res=res+toString(rightChild(node),indentation+" ");
    }
    
  return res;    
}

Pascal Schärli 09.10.2020

Vorlesung

Pascal Schärli 09.10.2020

String vs StringBuffer

  • Klasse String
    • immutable: Unveränderlich
    • final -> Operationen können gut optimiert werden (Zb. multithreading)
  • Klasse StringBuffer
    • mutable: veränderbar
    • Mehr Platz
    • Gewisse Operationen sind aufwendiger

Pascal Schärli 09.10.2020

String vs StringBuffer

String myString = "hello";
myString = myString + " world";
StringBuffer myStringBuffer = "hello";
myStringBuffer.append(" world");
"hello"
" world"
"hello world"
"hello"
" world"
"hello world"

Pascal Schärli 09.10.2020

Garbage Collector

String myString = "hello";
myString = myString+" world";
myString = myString+" how";
myString = myString+" are";
myString = myString+" you";
myString = myString+" today";
"hello"
" world"
"hello world"
" how"
"hello world how"
"hello world how are"
" you"
"hello world how are you"
" are"

Pascal Schärli 09.10.2020

Garbage Collector

String myString = "hello";
myString = myString+" world";
myString = myString+" how";
myString = myString+" are";
myString = myString+" you";
myString = myString+" today";
"hello world how are you"
" today"
"hello world how are you today"

Pascal Schärli 09.10.2020

Schleifeninvarianten

static int divide(int in, int div){

    assert(in >= 0 && div >= 0);
    
    int n = in;
    int out = 0;
    
    // [Vor Schleife]
    while(n >= div){
        // [Vor Schleifenkörper]
        out += 1;
        n -= div;
        // [Nach Schleifenkörper]
    }
    // [Nach Schleife]

    return out;
}

Schleifeninvarianten sind ein Weg um die Korrektheit einer Funktion zu beweisen.

Definition:

  1. Falls die Schleifeninvariante vor dem Schleifenkörper gilt, so gilt sie auch nach dem Schleifenkörper.
  2. Wenn man dann zeigen kann, dass die Invariante vor der Schleife gilt, so gilt sie auch nach der Schleife.

Schleife

Schleifen Körper

Pascal Schärli 09.10.2020

Schleifeninvarianten

Programmverifikation

Pascal Schärli - PVK Informatik II 2020

Schleifen Körper

Schleife

  1. Falls die Schleifeninvariante vor dem Schleifenkörper gilt, so gilt sie auch nach dem Schleifenkörper.
  2. Falls man zeigen kann, dass die Invariante vor der Schleife gilt, so gilt sie auch nach der Schleife.

Definition:

Schleifeninvarianten sind ein Weg um die Korrektheit einer Funktion zu beweisen.

static int f(int i, int j) {

   assert(i >= 0 && j >= 0);
   
   int u = i;
   int z = 0;
   
   // [Vor Schleife]
   while (u > 0){
        // [Vor Schleifenkörper]
        z = z + j;
        u = u - 1;
        // [Nach Schleifenkörper]
   }
   // [Nach Schleife]

   return z; 
}

Schleifeninvarianten

1. Beweise, dass dies eine korrekte Scheifeninvariante ist:

in = n + out * div && n >= 0 && (in  - n) % div = 0
static int divide(int in, int div){

    assert(in >= 0 && div >= 0);
    
    int n = in;
    int out = 0;
    
    // [Vor Schleife]
    while(n >= div){
        // [Vor Schleifenkörper]
        out += 1;
        n -= div;
        // [Nach Schleifenkörper]
    }
    // [Nach Schleife]

    return out;
}

Vor Schleifenkörper

  1. \(in = n_n + out_n \cdot div\)
    && \( n_n >=0\)
    && \((in  - n_n) \% div = 0\)

  2. \(n_n >= div\)


Nach Schleifenkörper

  1. \(in = (n_{n+1}+div) + (out_{n+1}-1)*div\)
    \(\Leftrightarrow in = n_{n+1} + out_{n+1} * div\)
  2. (n_{n+1}+div) >= div
    \(\Leftrightarrow\) n >= 0
  3. \((in - (n_{n+1}+div)) \% div = 0\)
    \(\Leftrightarrow (in - n_{n+1}) \% div = 0\)

(Schleifeninvariante)

(Sonst wären wir nicht in den while-loop gekommen)

\(\Rightarrow\) Schleifeninvariante gilt auch nach Schleifenkörper

Pascal Schärli 09.10.2020

Schleifeninvarianten

1. Beweise, dass dies eine korrekte Scheifeninvariante ist:

in = n + out * div && n >= 0 && (in  - n) % div = 0
static int divide(int in, int div){

    assert(in >= 0 && div >= 0);
    
    int n = in;
    int out = 0;
    
    // [Vor Schleife]
    while(n >= div){
        // [Vor Schleifenkörper]
        out += 1;
        n -= div;
        // [Nach Schleifenkörper]
    }
    // [Nach Schleife]

    return out;
}

Vor Schleifenkörper

  1. \(in = n_n + out_n \cdot div\)
    && \( n_n >=0\)
    && \((in  - n_n) \% div = 0\)

  2. \(n_n >= div\)


Nach Schleifenkörper

  1. \(in = (n_{n+1}+div) + (out_{n+1}-1)*div\)
    \(\Leftrightarrow in = n_{n+1} + out_{n+1} * div\)
  2. (n_{n+1}+div) >= div
    \(\Leftrightarrow\) n >= 0
  3. \((in - (n_{n+1}+div)) \% div = 0\)
    \(\Leftrightarrow (in - n_{n+1}) \% div = 0\)

(Schleifeninvariante)

(Sonst wären wir nicht in den while-loop gekommen)

\(\Rightarrow\) Schleifeninvariante gilt auch nach Schleifenkörper

Pascal Schärli 09.10.2020

Schleifeninvarianten

2. Zeige, dass die Schleifeninvariante vor der Schleife gilt

in = n + out * div && n >= 0 && (in  - n) % div = 0
static int divide(int in, int div){

    assert(in >= 0 && div >= 0);
    
    int n = in;
    int out = 0;
    
    // [Vor Schleife]
    while(n >= div){
        // [Vor Schleifenkörper]
        out += 1;
        n -= div;
        // [Nach Schleifenkörper]
    }
    // [Nach Schleife]

    return out;
}
  1. in = n + out * div
    in = in + 0 * div
    in = in ✓
     
  2. n >= 0
    in >= 0 ✓
     
  3. (in - n) % div = 0
    (in - in) % div = 0
    0 % div = 0 ✓

1.

2.

3.

Pascal Schärli 09.10.2020

Schleifeninvarianten

3. Daraus folgt, dass sie auch nach der Schleife gilt.

static int divide(int in, int div){

    assert(in >= 0 && div >= 0);
    
    int n = in;
    int out = 0;
    
    // [Vor Schleife]
    while(n >= div){
        // [Vor Schleifenkörper]
        out += 1;
        n -= div;
        // [Nach Schleifenkörper]
    }
    // [Nach Schleife]

    return out;
}
  1. in = n + out * div
&& n >= 0
&& (in  - n) % div = 0
  2. n < div
in = n + out * div && n >= 0 && (in  - n) % div = 0

Daraus folgt:

  1. 0 <= n < div
    && (in - n) % div = 0
    && out = (in - n) / div
  2. \(\Rightarrow\) out = ⌊in / div⌋

(Schleifeninvariante)

(Sonst wären wir nicht aus dem while-loop gekommen)

Pascal Schärli 09.10.2020

Schleifeninvarianten

Wie findet man eine Schleifeninvariante?

  • Es gibt keinen Weg eine Schleifeninvariante zu finden, welche den gewünschten Beweis ermöglicht.
     
  • Es ist nur möglich zu prüfen ob eine Gegebene Invariante funktioniert.
     
  • Probiert eine Invariante aus, schaut ob der Beweis funktioniert.
     
  • Falls nicht, passt eure Invariante an und versucht es nochmals, bis es funktioniert.

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots
  • Gleiches Konzept wie BNF
  • Ein Ausdruck ist erzeugbar, wenn es einen Weg durch das Diagramm gibt, welcher diesen beschreibt

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxdiagramme

Knoten

Unterbäume

Baum

(

)

Baum

Unterbäume

,

Knoten

B

A

C

Z

\cdots 
A(B(C,D))

Pascal Schärli 09.10.2020

Syntaxchecker

Var

Clause

(

)

+

private static int parseClause(String kd, int offset) throws ParseException {
    if (!checkNext('(', kd, offset)) {
        throw new ParseException("expected '('", offset);
    }
    offset++;
    
    while(true){
        offset = parseVar(kd, offset);
        if (!checkNext('+', kd, offset)) {
            break;
        }
        offset++;    
    }
    
    if (!checkNext(')', kd, offset)) {
        throw new ParseException("expected ')'", offset);
    }
    offset++;

    return offset;
}

parst '('

parst Var

falls kein '+' folgt, Schleife abbrechen

sonst offset erhöhen ('+' parsen)

parst ')'

neuen offset zurückgeben

Pascal Schärli 09.10.2020

Pascal Schärli 09.10.2020

int j = 9;
int i = 0;

while(i < 9){
    i++;
    j--;
}
  1. i == 9
  2. j == 9
  3. i + j == 9
  4. i - j == 9

Welches ist die korrekte Schleifeninvariante?

Pascal Schärli 09.10.2020

int a = 0;
int b = 0;

while(b < 7){
    b++;
    a += 10;
}
  1. a == b + 10
  2. a == b * 10
  3. b == a - 10
  4. b == 0

Welches ist die korrekte Schleifeninvariante?

Pascal Schärli 09.10.2020

int info = -1;
int II = 1;

while(info < 2){
    info++;
}
  1. info - II == -2

  2. info + II == 0
  3. info*II <3
  4. info / II < 2

Welches ist die korrekte Schleifeninvariante?

Pascal Schärli 09.10.2020

Welcher Jodel ist falsch?

Start

Mitte

Ende

Jodel

Start

j

o

Mitte

du

de

Ende

l

i

  1. jodududeli
  2. jodudedudelii
  3. jooodudeliii
  4. jodududedeli

Pascal Schärli 09.10.2020

Mit welcher "Mitte" kann man
"jodeli" darstellen?

Start

Mitte

Ende

Jodel

Start

j

o

Mitte 1

du

de

Ende

l

i

Mitte 2

du

de

Mitte 3

du

de

Mitte 4

du

de

Pascal Schärli 09.10.2020

Welches Syntaxdiagramm wird von diesem Programm geprüft?

private static int parseStart(String kd, int offset) throws ParseException{
    
    if(checkNext('j', kd, offset)){
        offset++;
    }
    else{
        throw ParseException("Expected \"j\" at "+offset);
    }
    
    while(checkNext('o', kd, offset)){
        offset++;
    }
    
    return offset;
}

Start 1

j

o

Start 2

j

o

Pascal Schärli 09.10.2020

Vorbesprechung

Pascal Schärli 09.10.2020

Programmverifikation

  1. Findet eine Schleifeninvariante.

  2. Beweist mittels der gefundenen Schleifeninvariante die Korrektheit der Implementierung.

  3. Gilt nach der Änderung an Zeilen 5,6 noch die Schleifeninvariante?
    Ist der Beweis immer noch gültig?

static int f(int i, int j) {
   int u = i;
   int z = 0;
   while (u > 0){
      z = z;
      u = u;
   }
   return z; 
}
static int f(int i, int j) {
   int u = i;
   int z = 0;
   while (u > 0){
      z = z + j;
      u = u - 1;
   }
   return z; 
}

Tipp: Der Beweis ist recht ähnlich zu meinem Beispiel im BestOf

Pascal Schärli 09.10.2020

String und StringBuffer

Caesar-Verschlüsselung

  • Buchstaben werden um 3 weitergesetzt.
    • Geheimniss
      \(\rightarrow\)Jhklpqlvv
  • Chars können durch Integeroperationen nach ASCII modifiziert werden.
    • 'A' + 1 == 'B'
    • 'A' + '$' == 'e'

Pascal Schärli 09.10.2020

String und StringBuffer

public static String encrypt(String s) {
    String ret = "";
    for (int i = 0; i != s.length(); ++i) {
        ret = ret + (char) (s.charAt(i) + 3);
    }
    return ret;
}
public static String decrypt(String s) {
    // TODO
}
  • Die Funktion encrypt ist bereits gegeben, implementiert analog dazu die Funktion decrypt.
  • Verwendet StringBuffer in decrypt.
  • Der Rückgabewert sollte aber immer noch String sein
    \(\rightarrow\) .toString()

Pascal Schärli 09.10.2020

Syntaxdiagramm

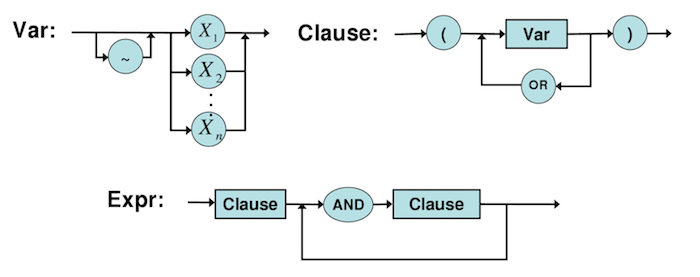
  • Sind die folgenden Strings korrekte Clauses?
    1. \(X_2\)
    2. \((\sim X_1)\)
    3. \(\sim(X_1 ~OR \sim X_2)\)
    4. \((X_2)~OR~(\sim X_1 ~ OR ~ X_2)\)
       
  • Sind die folgenden Strings korrekte Expressions?
  1. \((X_1~OR~X_2)~AND~(\sim X_2)\)
  2. \((X_1)~AND~(\sim X_1 ~OR~ \sim X_2) ~AND~ (X_2)\)

Pascal Schärli 09.10.2020

Syntaxdiagramm für Bäume

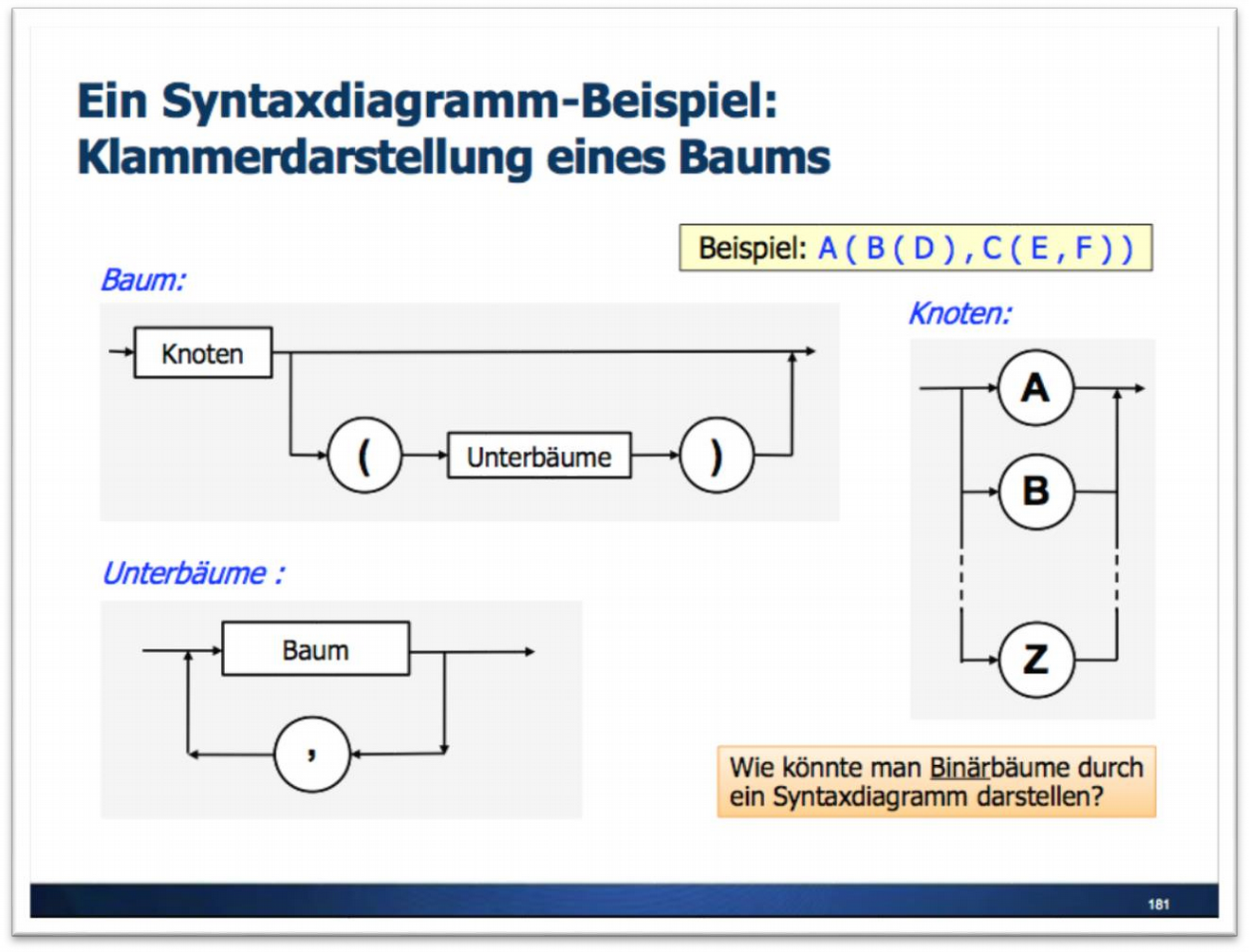
  • Ergänzen Sie das Syntaxdiagramm , sodass leere Bäume und leere Teilbäume generiert werden können.
  • Ein leerer Baum bzw. Teilbaum soll dabei durch ein ‘-’ repräsentiert werden.

Pascal Schärli 09.10.2020

Syntaxchecker

  • Implementiert einen Syntaxchecker für Wurzelbäume in der Klammerdarstellung.
     
  • Tipp: Verwendet die folgenden Funktionen:
//checks if the char at position offset in the String kd is equal to c
Boolean checkNext(char c, String kd, int offset){ ... }
int parseTree(String kd, int offset){ ... }
int parseSubtree(String kd, int offset) { ... }
int parseNode(String kd, int offset){ ... }

Pascal Schärli 09.10.2020

Viel Spass!

Pascal Schärli 09.10.2020