Informatik II PVK
Pascal Schärli

Voraussetzungen
Pascal Schärli - PVK Informatik II 2021

Primitive Datentypen
Voraussetzungen
- boolean
- True / False
- char
- Ascii Character
- byte
- 8 bit Ganzzahl
- short
- 16 bit Ganzzahl
- int
- 32 bit Ganzzahl
- long
- 64 bit Ganzzahl
- float
- 32 bit Fliesskommazahl
- double
- 64 bit Fliesskommazahl
Pascal Schärli - PVK Informatik II 2021
Primitive Datentypen
Voraussetzungen
| boolean | char | byte | short | int | long | float | double | |
|---|---|---|---|---|---|---|---|---|
| boolean | ||||||||
| char | ||||||||
| byte | ||||||||
| short | ||||||||
| int | ||||||||
| long | ||||||||
| float | ||||||||
| double |
int
int
int
int
long
float
double
int
int
int
long
float
double
int
int
int
int
int
int
int
int
int
long
long
long
long
long
long
long
float
float
float
float
float
float
float
float
float
double
double
double
double
double
double
double
double
double
double
double
a + b = c
a
b
- Mit Booleans kann nicht gerechnet werden
- Das Resultat ist mindestens ein int
- Das Resultat hat immer den allgemeineren Typ
Pascal Schärli - PVK Informatik II 2021
Increment
Voraussetzungen
6
Wert von a
5
Output
6
Wert von a
6
Output
int a = 5;
System.out.println(a++);int a = 5;
System.out.println(++a);Die Variabel wird erhöht und der alte Wert wird zurückgegeben
Die Variabel wird erhöht und der neue Wert wird zurückgegeben
Post Increment
Pre Increment
- Der Pre- Post Increment Operator erhöht eine Variable um 1.
- Man kann das Increment vor oder nach der Variabel schreiben.
Pascal Schärli - PVK Informatik II 2021
Voraussetzungen
Scopes
8
8int a = 2;
if (x < 7) {
a = 8;
System.out.println(a);
}
System.out.println(a);
8
2int a = 2;
if (x < 7) {
int a = 8;
System.out.println(a);
}
System.out.println(a);
Pascal Schärli - PVK Informatik II 2021
Voraussetzungen
public static void printListElements(ArrayList<Integer> list) {
for (int i = 0; i < list.size(); i++) {
System.out.println(list.get(i));
}
}For-Each-Loop
public static void printListElements(ArrayList<Integer> list) {
for (Integer k : list) {
System.out.println(k);
}
}For-Loops können kompakter notiert werden, falls man über alle Elemente einer Liste iterieren will:
Pascal Schärli - PVK Informatik II 2021
Voraussetzungen
1 2 4 8 int i = 1;
do{
System.out.println(i + " ");
i*=2;
} while(i < 10);- Alternative zum while-Loop
- Kondition wird erst am Ende geprüft
- Schleifenkörper wird mindestens ein Mal ausgeführt
Do-While-Loop
Pascal Schärli - PVK Informatik II 2021
Voraussetzungen
0 2 4 6 8for (int i = 0; i < 10; i++) {
if (i % 2 != 0)
continue;
System.out.print(i + " ");
}- Das Keyword "continue" bricht die Loop-Iteration ab.
- Die Ausführung vom Schleifenkörper wird abgebrochen und die nächste Iteration wird gestartet.
Continue
Pascal Schärli - PVK Informatik II 2021
Voraussetzungen
0for (int i = 0; i < 10; i++) {
if (i % 2 != 0)
break;
System.out.print(i + " ");
}- Das Keyword "break" bricht den ganzen Loop ab.
- Die Ausführung der ganzen Schleife wird abgebrochen und das Programm geht nach der Schleife weiter.
Break
Pascal Schärli - PVK Informatik II 2021
Ternary Operator
Voraussetzungen
- In Java ist "?" ein Operator, welchen man als Abkürzung von einem if-else Statement verstanden werden kann
- Die Syntax ist <boolean> ? <value1> : <value2>
- Der Output ist <value1> falls der boolean true war, ansonsten ist der Output <value2>.
- Beispiel:
boolean y = true;
String s = y ? "y was true" : "y was false";
System.out.println(s);y was truePascal Schärli - PVK Informatik II 2021
int foo(int a, float b, boolean c){
if(c){
a += b;
}
else{
a-=b;
}
return a;
}Datentyp vom Rückgabewert
Name der Funktion
Beliebig viele Übergabewerte
Funktions-Körper (Berechnung)
Rückgabe des Resultats
Funktionen
Voraussetzungen
Pascal Schärli - PVK Informatik II 2021
/**
* Checks wether x is within the interval [left, right]
*
* @param x
* @param left The left edge of the interval
* @param right The right edge of the interval
* @return true iff x is in the interval [left, right]
* @throws IllegalArgumentException if the interval is empty
*/
boolean inInterval(double x, double left, double right){
if(left > right){
throw new IllegalArgumentException("Empty Interval");
}
return x >= left && x <= right;
}
Javadoc
Voraussetzungen
Pascal Schärli - PVK Informatik II 2021
Prüfungs Statistiken
Pascal Schärli - PVK Informatik II 2021
Prüfungsstatistiken
Generell
- Bei Informatik 2 sind die Prüfungen weniger konsistent als bei Informatik 1
- Ihnen ist es wichtig immer wieder neue und frische Aufgaben zu machen, und kennen alle Prüfungen weche auf AMIV veröffentlicht sind.
- Trotzdem gibt es einige Aufgabentypen, welche fast jedes Jahr kommen, wenn auch in leicht abgeänderter Form.
- Daher denke ich, dass das Lösen von alten Prüfungen trotzdem eine gute Vorbereitung ist, auch wenn sie sagen, dass es nicht so ist.
- Auf meiner Webseite habe ich alle einzelnen Prüfungsaufgaben mit Lösungen hochgeladen:
https://pascscha.ch/info2/pvk/pruefungen/
Pascal Schärli - PVK Informatik II 2021
Prüfungsstatistiken
Notenpunkte pro Kategorie
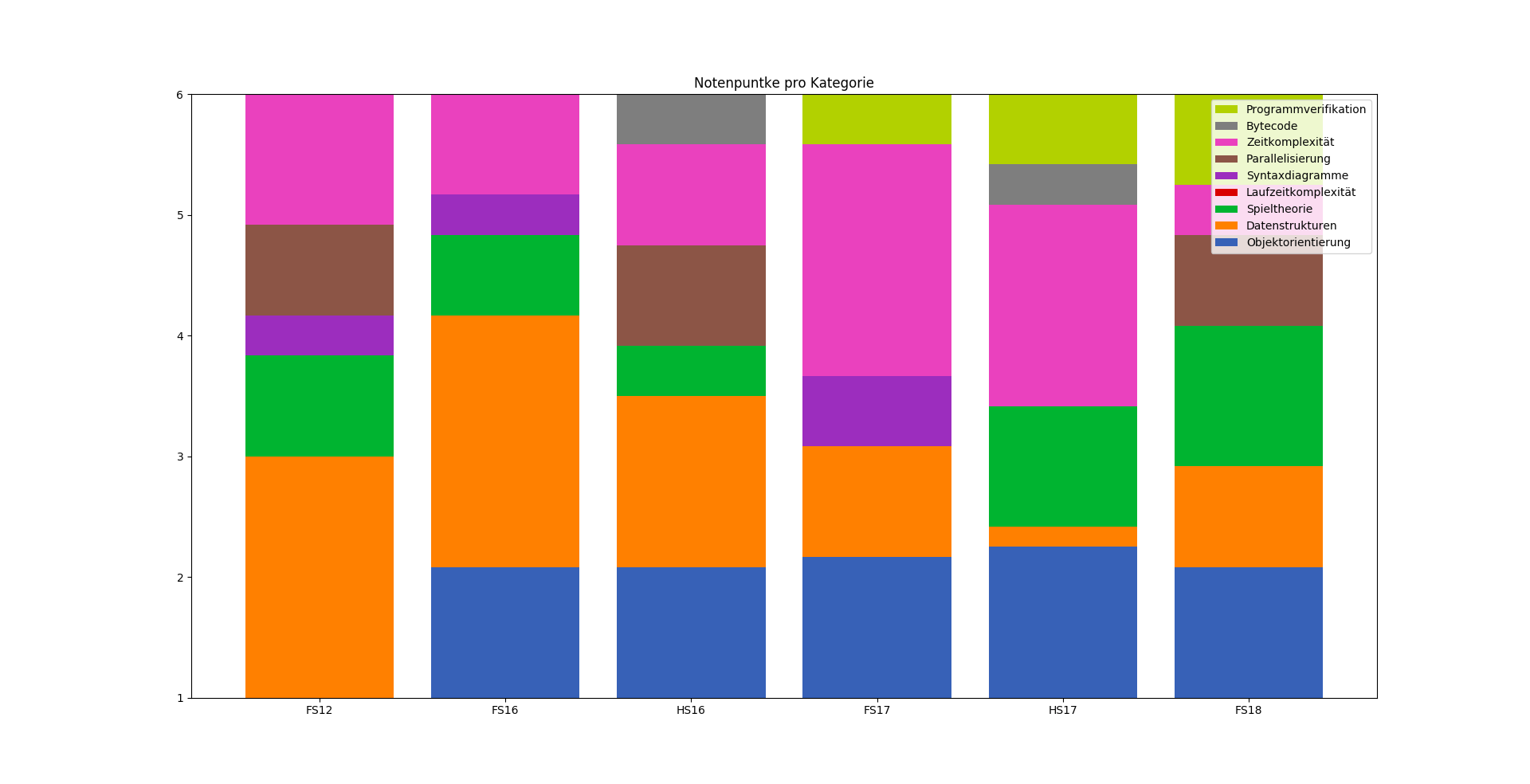
Pascal Schärli - PVK Informatik II 2021
Prüfungsstatistiken
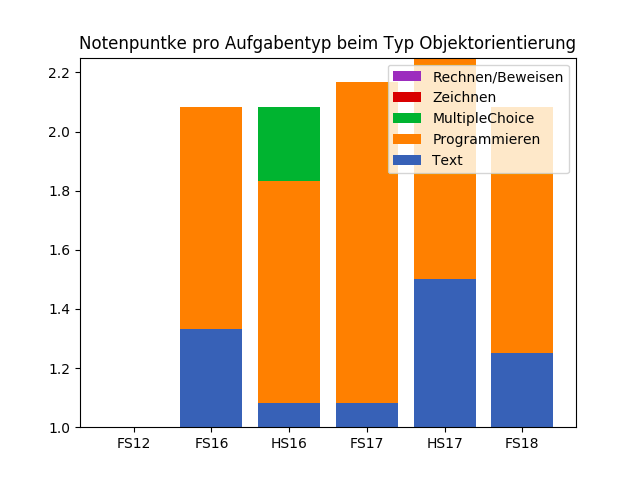
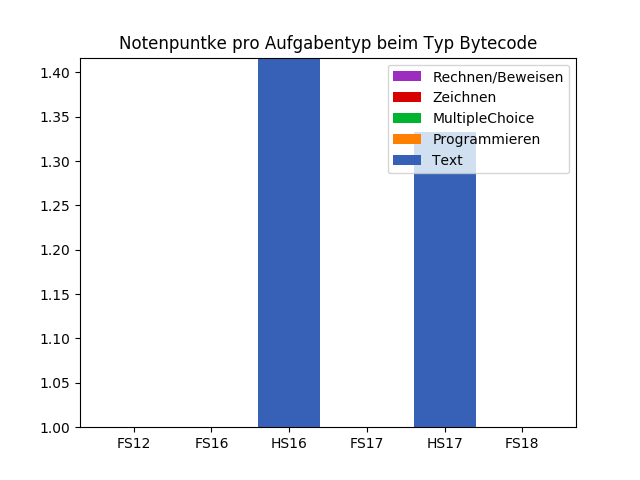
Notenpunkte pro Aufgabentyp
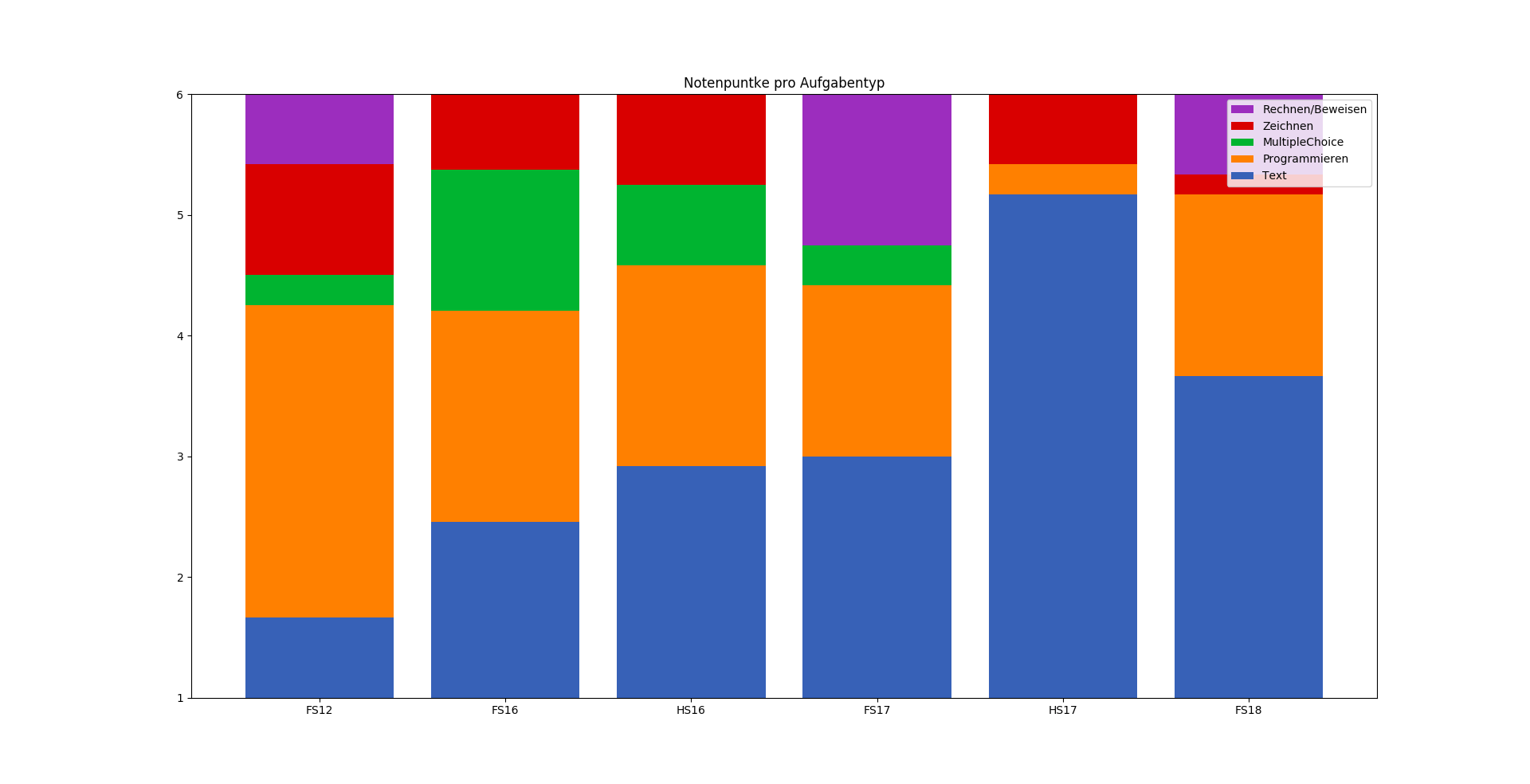
Pascal Schärli - PVK Informatik II 2021
Objektorientierung

Pascal Schärli - PVK Informatik II 2021
Objektorientierung
Call by Reference
- In C++ war beides möglich:
- Call by value: Daten werden kopiert und übergeben
- Call by reference: Referenz auf die Daten wird übergeben
- Java ist IMMER call by value!!
- Bei der Übergabe einer Referenz auf ein Objekt wird die Adresse in eine lokale Variable kopiert!
- Bei Übergabe eines primitiven Typs (char, int, float) wird der Wert in eine lokale Variable kopiert!
Pascal Schärli - PVK Informatik II 2021
public static void swap(StringBuffer sbf1, StringBuffer sbf2) {
StringBuffer temp = sbf1;
sbf1 = sbf2;
sbf2 =temp;
} StringBuffer sbf1 = new StringBuffer("Hello");
StringBuffer sbf2 = new StringBuffer("World");
System.out.println(sbf1+" "+sbf2);
swap(sbf1,sbf2);
System.out.println(sbf1+" "+sbf2); Hello World
Hello WorldOutput:
Broken Swap
Objektorientierung
Trotzdem dass beim Funktionsaufruf eine Referenz übergeben wird, werden die Stringbuffer nicht getauscht, warum?
Pascal Schärli - PVK Informatik II 2021
public static void swap(StringBuffer s1, StringBuffer s2){
StringBuffer temp = s1;
s1 = s2;
s2 =temp;
} StringBuffer sbf1 = new StringBuffer("Hello");
StringBuffer sbf2 = new StringBuffer("World");
System.out.println(sbf1+" "+sbf2);
swap(sbf1,sbf2);
System.out.println(sbf1+" "+sbf2);Output:
sbf1
address1
address1
"Hello"
address2
"World"
sbf2
address2
Hello World
Objektorientierung
Broken Swap
Pascal Schärli - PVK Informatik II 2021
public static void swap(StringBuffer s1, StringBuffer s2){
StringBuffer temp = s1;
s1 = s2;
s2 =temp;
} StringBuffer sbf1 = new StringBuffer("Hello");
StringBuffer sbf2 = new StringBuffer("World");
System.out.println(sbf1+" "+sbf2);
swap(sbf1,sbf2);
System.out.println(sbf1+" "+sbf2);
Hello World
Output:
sbf1
address1
address1
"Hello"
address2
"World"
sbf2
address2
s1
address1
s2
address2
swap
Objektorientierung
Broken Swap
Pascal Schärli - PVK Informatik II 2021
public static void swap(StringBuffer s1, StringBuffer s2){
StringBuffer temp = s1;
s1 = s2;
s2 =temp;
} StringBuffer sbf1 = new StringBuffer("Hello");
StringBuffer sbf2 = new StringBuffer("World");
System.out.println(sbf1+" "+sbf2);
swap(sbf1,sbf2);
System.out.println(sbf1+" "+sbf2);
Hello World
Output:
sbf1
address1
address1
"Hello"
address2
"World"
sbf2
address2
s1
address1
s2
address2
swap
Objektorientierung
Broken Swap
Pascal Schärli - PVK Informatik II 2021
public static void swap(StringBuffer s1, StringBuffer s2){
StringBuffer temp = s1;
s1 = s2;
s2 =temp;
} StringBuffer sbf1 = new StringBuffer("Hello");
StringBuffer sbf2 = new StringBuffer("World");
System.out.println(sbf1+" "+sbf2);
swap(sbf1,sbf2);
System.out.println(sbf1+" "+sbf2);Output:
sbf1
address1
address1
"Hello"
address2
"World"
sbf2
address2
Objektorientierung
Broken Swap
Pascal Schärli - PVK Informatik II 2021
Hello World
Hello Worldpublic static void swap(StringBuffer s1, StringBuffer s2) {
StringBuffer temp = new StringBuffer(s1);
s1.delete(0, s1.length());
s1.append(s2);
s2.delete(0, s2.length());
s2.append(temp);
} StringBuffer sbf1 = new StringBuffer("Hello");
StringBuffer sbf2 = new StringBuffer("World");
System.out.println(sbf1+" "+sbf2);
swap(sbf1,sbf2);
System.out.println(sbf1+" "+sbf2);
Hello World
Output:
sbf1
address1
address1
"Hello"
address2
"World"
sbf2
address2
Hello World
World Hellos1
address1
s2
address2
swap
"Hello"
"World"
\(\rightarrow\) Man kann das zu Grunde liegende Objekt verändern!
Objektorientierung
Fixed Swap
Pascal Schärli - PVK Informatik II 2021
Pakete
Objektorientierung
{1, 4, 21, 8}
→ “1, 4, 21, 8, null“
Lists.java
package u5a1;
import node.Node;
public class Lists {
public static String toString(Node node) {
if (node == null) return "null";
StringBuffer buf = new StringBuffer();
buf.append(node.value).append(", ").append(toString(node.next));
return buf.toString();
}
}Node.java
package node;
public class Node {
public int value;
public Node next;
public Node(int value, Node next) {
this.value = value;
this.next = next;
}
}Pascal Schärli - PVK Informatik II 2021
Keywords
Objektorientierung
- final: Darf nicht verändert werden
- public: Für alle Sichtbar
- private: In der Klasse Sichtbar
- protected: in abgeleiteten Klassenund im package Sichtbar
- static: unabhängig von der Klasseninstanz, existiert nur einmal für alle Objekte dieser Klasse
- Ohne Modifier: Im package sichtbar
public class Impedance {
private final String name;
protected double real, imag;
int i;
public Impedance(String name, double real,
double imag) {
this.name = name;
this.real = real;
this.imag = imag;
}
public static Impedance add(String name,
Impedance z1, Impedance z2) {
double real = z1.getReal() + z2.getReal();
double imag = z1.getImag() + z2.getImag();
return new Impedance(name, real, imag);
}
public String toString() {
return getName() + " = " + getReal() +
" + i" + getImag();
}
public String getName() {
return this.name;
}
public double getImag() {
return this.imag;
}
public double getReal() {
return this.real;
}
}Pascal Schärli - PVK Informatik II 2021
- In Java ist es möglich, dass eine Klasse von einer anderen Klasse "erbt".
- Die erbende Klasse erbt somit alle Funktionen und Attribute und kann diese noch erweitern.
- Dies ermöglicht es gewisse Typen und Strukturen besser zu modellieren.
Polymorphie
Objektorientierung
Pascal Schärli - PVK Informatik II 2021
public class Fahrzeug{
int radzahl;
public Fahrzeug(int radzahl){
this.radzahl = radzahl;
}
} public class Auto extends Fahrzeug{
protected float hubraum;
public Auto(float hubraum){
super(4);
this.hubraum = hubraum;
}
public float getHubraum(){
return hubraum;
}
public void setHubraum(float hubraum){
if(hubraum>0) this.hubraum = hubraum;
}
} public class Lastwagen extends Auto{
float capacity;
public Lastwagen(float hubraum,
float capacity){
super(hubraum);
this.capacity = capacity;
}
} public class Fahrrad extends Fahrzeug{
public Fahrrad(){
super(2);
}
}Fahrzeug
Auto
Lastwagen
Fahrrad
Objektorientierung
Polymorphie
Pascal Schärli - PVK Informatik II 2021
Fahrzeug myFahrrad = new Fahrrad();
System.out.println(myFahrrad.radzahl);
myFahrrad.setHubraum(300);
Fahrzeug myLastwagen = new Lastwagen(80000,50);
System.out.println(myLastwagen.radzahl);
myLastwagen.setHubraum(300);
Output: 4
Output: 2
Compile Error:
The method setHubraum(int) is undefined for the type Fahrzeug
Compile Error:
The method setHubraum(int) is undefined for the type Fahrzeug
Fahrzeug
Auto
Lastwagen
Fahrrad
Polymorphie
Objektorientierung
Pascal Schärli - PVK Informatik II 2021
- Warum können wir den Hubraum von myLastwagen nicht bestimmen, obwohl es ein Objekt vom Typ Lastwagen ist?
- Beim Erstellen von myLastwagen haben wir gesagt, dass es vom Typ Fahrzeug ist:
- myLastwagen hat also alle Attribute von einem Lastwagen, man kann sie einfach nicht abrufen.
- \(\Rightarrow\) Type Casts
Fahrzeug myLastwagen = new Lastwagen(80000,50);((Lastwagen)myLastwagen).setHubraum(300);Objektorientierung
Polymorphie
Pascal Schärli - PVK Informatik II 2021
Fahrzeug myLastwagen = new Lastwagen(80000,50);
System.out.println(myLastwagen.radzahl);
((Lastwagen)myLastwagen).setHubraum(300);
Fahrzeug myFahrrad = new Fahrrad();
System.out.println(myFahrrad.radzahl);
((Lastwagen)myFahrrad).setHubraum(300);
Runtime Error:
Exception in thread "main" java.lang.ClassCastException: Fahrzeug cannot be cast to Lastwagen
Fahrzeug
Auto
Lastwagen
Fahrrad
Objektorientierung
Polymorphie
Pascal Schärli - PVK Informatik II 2021
- Falls ihr auf ein Attribut zugreifen möchtet, welches nicht existiert oder nicht abrufbar ist, gibt es einen Compile Error
- Falls ihr einen Cast machen wollt, welcher nicht funktioniert, gibt es einen Runtime Error
Fahrzeug myLastwagen = new Lastwagen(80000, 50);
myLastwagen.setHubraum(300);Fahrzeug myFahrrad = new Fahrrad();
((Lastwagen)myFahrrad).setHubraum(300);Polymorphie
Objektorientierung
Fahrrad
Lastwagen
Auto
Fahrzeug
Pascal Schärli - PVK Informatik II 2021
class Mensch { ... }class ETHStudent extends Student { String legiNr; }class ITETStudent extends ETHStudent { ... }class Student extends Mensch { ... }Student tim = new ETHStudent();Object obj = tim;
Mensch mensch = tim;
Student student = tim;
ETHStudent ethStud = (ETHStudent) tim;
ITETStudent itetStud = (ITETStudent) tim;Java denkt es ist ein Student
Wir wissen, es ist ein ETHStudent
ohne cast
mit cast
Runtime Error
zuweisung möglich ohne Cast
zuweisung möglich ohne Cast
zuweisung möglich mit Cast
Runtime Error
jede Java Klasse erbt von Object
Objektorientierung
Polymorphie
Pascal Schärli - PVK Informatik II 2021
class Mensch { ... }class ETHStudent extends Student { String legiNr; }class ITETStudent extends ETHStudent { ... }class Student extends Mensch { ... }Student tim = new ETHStudent();Mensch mensch = tim;
Student student = tim;
ETHStudent ethStud = (ETHStudent) tim;
ITETStudent itetStud = (ITETStudent) tim;
System.out.println(mensch.legiNr);
System.out.println(student.legiNr);
System.out.println(ethStud.legiNr);
System.out.println(itetStud.legiNr);Compile Error
Compile Error
Kein Compile Error
Kein Compile Error
haben legiNr
Polymorphie
Objektorientierung
Pascal Schärli - PVK Informatik II 2021
- Falsche Type-Casts können zu Runtime-Error führen.
- Wie können wir das verhindern?
- instanceof Operator gibt zurück, ob ein Objekt gecasted werden kann.
Student tim = new ETHStudent();
System.out.println(tim instanceof Mensch);
System.out.println(tim instanceof Student);
System.out.println(tim instanceof ETHStudent);
System.out.println(tim instanceof ITETStudent);
true
true
true
falseOutput:
instanceof
Objektorientierung
Pascal Schärli - PVK Informatik II 2021
- In einer Abstrakten Klasse kann man Methoden implementieren, aber auch nur deklarieren.
- Man kann keine Abstrakten Objekte instanzieren (weil man sonst unimplementierte Methoden aufrufen könnte)
- Eine Klasse kann höchstens eine Abstrakte Klasse erweitern
public abstract class AbstractStack {
// declare abstract functions
public abstract void push();
public abstract int pop();
public abstract int peek();
public abstract int size();
// already implement some functions
public boolean isEmpty(){
return size() == 0;
}
}public class Stack extends AbstractStack {
// declare abstract functions
public void push(){/*TODO*/}
public int pop(){/*TODO*/}
public int peek(){/*TODO*/}
public int size(){/*TODO*/}
}Abstrakte Klassen
Objektorientierung
Pascal Schärli - PVK Informatik II 2021
- In einem Interface kann man keine Methoden implementieren, nur nur deklarieren.
- Man kann keine Interfaces instanzieren (weil man sonst unimplementierte Methoden aufrufen könnte)
- Eine Klasse kann mehrere Interfaces implementieren.
public Interface IStack {
// declare abstract functions
public void push();
public int pop();
public int peek();
public int size();
}public class Stack implements IStack {
// declare abstract functions
public int push(){/*TODO*/}
public int pop(){/*TODO*/}
public int peek(){/*TODO*/}
public int size(){/*TODO*/}
}Interfaces
Objektorientierung
Pascal Schärli - PVK Informatik II 2021
- Julia und Carina arbeiten mit Bäumen.
- Um gleichzeitig daran zu arbeiten implementiert Carina den Baum und Julia schreibt das Programm.
- Sie entscheiden sich: Sie verwenden einen ArrayTree
- Nach der Hälfte der Zeit merkt Carina, dass ein ListTree besser geeignet wäre.
- Carina sagt Julia, sie solle doch schnell alle Verwendungen von ArrayTree zu ListTree ändern.

Carina

Julia


Benutze ArrayTree
Meinung geändert, benutze ListTree
Objektorientierung
Factories
Pascal Schärli - PVK Informatik II 2021
Objektorientierung
Pascal Schärli - PVK Informatik II 2021
- Um solche Katastrophen zu verhindern benutzen wir Interfaces und Factories
- Julia benutzt eine "TreeFactory" um Bäume zu erstellen, welche dieses Interface implementieren.
interface ITree{
public ITree leftChild();
public ITree rightChild();
public int getValue();
public int setValue();
}public class TreeFactory {
public static ITree makeTree(){
return new ListTree();
}
}Tree Interface
Tree Factory
public class FancyCode {
public ArrayTree important(){
ArrayTree myRoot = new ArrayTree();
myRoot.setValue(4);
return myRoot;
}
}Julias Code Vorher
public class FancyCode {
public ITree important(){
ITree myRoot = TreeFactory.makeTree();
myRoot.setValue(4);
return myRoot;
}
}Julias Code Jetzt
Factories
ArrayList myList = new ArrayList();
myList.add(42);
myList.add(“I <3 Info II”);
int i = (Integer)myList.get(0);
String s = (String)myList.get(1);ArrayList Kann beliebige Typen speichern:
- Flexibel, aber Casts sind gefährlich
- Falls man nicht mehr weiss, was wo in der Liste ist, kann es zu Chaos führen
- \(\rightarrow\) Generics
Objektorientierung
Generics
Pascal Schärli - PVK Informatik II 2021
ArrayList<Integer> myList = new ArrayList<Integer>();
myList.add(42);
int i = myList.get(0);
myList.add(“Hello World”);Man kann einer ArrayList sagen, dass sie nur einen bestimmten Typ speichern darf:
- Vorteile:
- Typsicherheit
- keine Casts nötig
- Nachteile:
- Weniger Flexibel
Compile-Error
Objektorientierung
Generics
Pascal Schärli - PVK Informatik II 2021
public class Tree<T> {
T value;
Tree right;
Tree left;
public Tree(T value) {
right = null;
left = null;
this.value = value;
}
public Tree<T> leftChild() {
return left;
}
public Tree<T> rightChild() {
return right;
}
}Tree<Integer> tree1 = new Tree<Integer>(5);
tree1.left = new Tree<Integer>(3);
tree1.right = new Tree<Integer>(6);
Tree<String> tree2 = new Tree<String>("root");
tree2.right = new Tree<String>("right");
tree2.left = new Tree<String>("left");5
3
6
"root"
"left"
"right"
tree1
tree2
Objektorientierung
Generics
Pascal Schärli - PVK Informatik II 2021
Herbst 2017, 1.17 Notenpunkte
Objektorientierung
Prüfungsaufgabe
Pascal Schärli - PVK Informatik II 2021
Objektorientierung
Prüfungsaufgabe
Herbst 2017, 1.17 Notenpunkte
public class Activity{
private String name;
private double duration;
private double rating;
public Activity(String name, double duration, double rating) {
if(duration <= 0) {
throw new IllegalArgumentException("The duration can not be negative!");
}
if(rating < 0 || rating > 5) {
throw new IllegalArgumentException("The rating has to be between 0 and 5!");
}
this.name = name;
this.duration = duration;
this.rating = rating;
}
public String getName() {
return name;
}
public double getDuration() {
return duration;
}
public double getRating() {
return rating;
}
}
Pascal Schärli - PVK Informatik II 2021
Objektorientierung
Prüfungsaufgabe
Herbst 2017, 1.17 Notenpunkte
public class Hike extends Activity {
private double difficulty;
public Hike(String name, double duration, double rating,
double difficulty) {
super(name, duration, rating);
if(difficulty < 1 || difficulty > 5) {
throw new IllegalArgumentException("The difficulty has to "
+ "be between 1 and 5!");
}
this.difficulty = difficulty;
}
public double getDifficulty() {
return difficulty;
}
}Pascal Schärli - PVK Informatik II 2021
Objektorientierung
Prüfungsaufgabe
Herbst 2017, 1.17 Notenpunkte
import java.util.ArrayList;
public class ActivityManager{
ArrayList<Activity> activities;
public ActivityManager() {
activities = new ArrayList<Activity>();
}
public void addActivitiy(Activity activity){
activities.add(activity);
}
public Hike findBestHike(double maxDuration, double maxDifference){
// [..]
}
}Pascal Schärli - PVK Informatik II 2021
Objektorientierung
Prüfungsaufgabe
Herbst 2017, 1.17 Notenpunkte
public Hike findBestHike(double maxDuration, double maxDifficulty){
Hike bestHike = null;
for (Activity activity : activities) {
if (activity instanceof Hike) {
Hike hike = (Hike) activity;
if (hike.getDuration() <= maxDuration
&& hike.getDifficulty() <= maxDifficulty) {
if (bestHike == null
|| hike.getRating() > bestHike.getRating()) {
bestHike = hike;
}
}
}
}
return bestHike;
}Pascal Schärli - PVK Informatik II 2021
Objektorientierung
Prüfungsaufgabe
Herbst 2017, 1.17 Notenpunkte
public class Main{
public static void main(String[] args){
ActivityManager = new ActivityManager();
// Adding activities
// Assume the parameter order for the Activity constructor is
// [name, duration, rating] and for the Hike constructor
// [name, duration, rating, difficulty]
manager.addActivitiy(new Activity("Spaziergang am See", 1.2, 2.5));
manager.addActivitiy(new Hike("Brunni - Kl. Mythen", 2, 4.5, 4.5));
manager.addActivitiy(new Activity("Velofahren Zuerich", 0.5, 1));
manager.addActivitiy(new Hike("Brunni - Gr. Mythen", 3, 3.5, 3.5));
manager.addActivitiy(new Activity("Schwimmen am Letten", 1, 4.5));
manager.addActivitiy(new Activity("Nichtstun", 0, 2.5));
manager.addActivitiy(new Hike("Weggis - Rigi Kulm", 5, 4, 3.5));
manager.addActivitiy(new Hike("Alpnach - Pilatus Kulm", 5, 5, 2));
double maxDuration = 4;
double maxDifficulty = 3.5;
Hike bestHike = manager.findBestHike(maxDuration, maxDifference);
System.out.println("Die beste Wanderung: " + bestHike.getName());
}
}Die beste Wanderung: Brunni - Gr. MythenPascal Schärli - PVK Informatik II 2021
Komplexität
Pascal Schärli - PVK Informatik II 2021
Komplexität
O-Notation
- Die O-Notation beschreibt, die Grössenordnung von einem Problem.
- Mathematische Definition:
- Sei \(g(n)\) der Aufwand vom Algorithmus.
- Dann ist \(g(n) \in O(f(n))\) falls
\(\exists n_0,c>0\) so dass \(\forall n > n_0 : g(n) \leq c \cdot f(n) \)
- Die Funkion darf also für genug grosse Inputs nur um einen Konstanten Faktor von der Komplexität abweichen.
- Im Endeffekt bedeutet das, dass wir nur den am schnellsten Wachsende Term betrachten müssen und alle konstanten Faktoren ignorieren können.
Pascal Schärli - PVK Informatik II 2021
Komplexität
O-Notation
Zeige, dass \(\frac{n^2 + 100}{2} \in O(n^2)\):
- \(g(n) = \frac{n^2 + 100}{2}\), \(f(n) = n^2\)
- Zu zeigen: \(\exists n_0,c>0\) so dass \(\forall n > n_0 : g(n) \leq c \cdot f(n) \)
- Wähle \(c = 1\)
- Finde \(n_0\)
- \(g(n) \leq c \cdot f(n)\)
- \(\Leftrightarrow \frac{n^2 + 100}{2} \leq n^2\)
- \(\Leftrightarrow 100 \leq n^2\)
- \(\Leftrightarrow n \geq 10\)
- \(\Rightarrow\) Wir können z.B \(n_0 = 10\) wählen.
- \(\Rightarrow \forall n > 10 : \frac{n^2 + 100}{2}\leq 1 \cdot n^2\)
- \(\Rightarrow \frac{n^2 + 100}{2} \in O(n^2)\)
Pascal Schärli - PVK Informatik II 2021
Komplexität
O-Notation
- Falls nicht nach Beweisen gefragt ist, müssen wir nicht all diese Rechnungen machen.
- Dann reicht es nur den am Schnellsten wachsenden Summanden zu betrachten und alle Konstanten Multiplikatoren zu ignorieren.
- Beispiele:
- \(\frac{1 +n^2 + n^5}{5}\)
- \(= \frac{1}{5} \cdot 1 + \frac{1}{5} \cdot n^2 + \frac{1}{5} \cdot n^5\)
- \(\in O(n^5)\)
- \(log(n^4) + log(n^3)\)
- \(= 7 \cdot log(n)\)
- \(\in O(log(n))\)
- \(\frac{1 +n^2 + n^5}{5}\)
Pascal Schärli - PVK Informatik II 2021
Komplexität
O-Notation
- Die O-Notation ist nur eine obere Schranke, das heisst falls ein Algorithmus \(\in O(n)\) ist, so ist er auch \(\in O(n^2)\).
- Falls also \(g(n) = \frac{n}{2}\) dann gilt sowohl \(g(n) \in O(n)\) als auch \(g(n) \in O(n^2)\)
- \(O(1) \in O(log(n)) \in O(n) \in O(n \cdot log(n))\)
\(\in O(n^2) \in O(n^{100}) \in O(2^n) \in O(n!)\)
Pascal Schärli - PVK Informatik II 2021
Komplexität
Laufzeitomplexität bestimmen
Zeile 5 Wird n-Mal Ausgeführt.
private static int f1(int n) {
int out = 0;
for(int i = 0; i < n; i++) {
out++;
}
return out;
}\(O(n)\)
Pascal Schärli - PVK Informatik II 2021
Komplexität
Laufzeitomplexität bestimmen
Zeile 5 Wird ca. \(\lfloor \frac{n}{5} \rfloor \)-Mal Ausgeführt.
\(O(n)\)
private static int f2(int n) {
int out = 0;
for(int i = 0; i * 5 < n; i++) {
out++;
}
return out;
}Pascal Schärli - PVK Informatik II 2021
Komplexität
Laufzeitomplexität bestimmen
Zeile 6 Wird \(n^2\)-Mal Ausgeführt.
\(O(n^2)\)
private static int f3(int n) {
int out = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++){
out++;
}
}
return out;
}Pascal Schärli - PVK Informatik II 2021
Komplexität
Laufzeitomplexität bestimmen
Zeile 6 Wird \(1000 * n\)-Mal Ausgeführt.
\(O(n)\)
private static int f4(int n) {
int out = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < 1000; j++){
out++;
}
}
return out;
}Pascal Schärli - PVK Informatik II 2021
Komplexität
Laufzeitomplexität bestimmen
Zeile 6 Wird \(\sum_{i=0}^{n-1}(i) = \frac{n*(n-1)}{2}\)-Mal Ausgeführt.
\(O(n^2)\)
private static int f5(int n) {
int out = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < i; j++){
out++;
}
}
return out;
}Pascal Schärli - PVK Informatik II 2021
Komplexität
Laufzeitomplexität bestimmen
- Zeile 4 macht, dass die inneren Loops \(n^2\)-Mal ausgeführt werden.
- Zeile 5 macht, dass der Innere Loop \(\sqrt{i} \approx n\)-Mal ausgeführt wird. Da dieser Loop selbst \(n^2\)-Mal wiederholt wird, sind das \(n^3\) Wiederholungen.
- Zeile 6 macht, dass die Instruktion \(j \cdot i \approx n^3\)-Mal ausgeführt wird. Da dieser Loop selbst ca \(n^3\)-Mal ausgeführt wird, ist die gesamte Komplexität \(O(n^6)\)
\(O(n^6)\)
private static int f5(int n) {
int out = 0;
for(int i = 0; i < n*n; i++) {
for(int j = 0; j*j < i; j++){
for(int k = j*i; k > 0; k--){
out++;
}
}
}
return out;
}Pascal Schärli - PVK Informatik II 2021
Komplexität
Speicherkomplexität bestimmen
- Neben der Laufzeit ist auch der benutzte Speicher einen Faktor, welchen man beim Entwickeln von einem Algorithmus im Auge behalten sollte.
- Den benötigten Speicher kann man genauso wie die Laufzeit mit der O-Notation beschreiben
Pascal Schärli - PVK Informatik II 2021
Komplexität
Speicherkomplexität
public static int fibo(int n) {
if (n <= 1) return 1;
return fibo1(n - 1) + fibo1(n - 2);
}Pascal Schärli - PVK Informatik II 2021
fibo(1) + fibo(0)
fibo(2) + fibo(1)
fibo(1) + fibo(0)
fibo(3) + fibo(2)
fibo(4)
Die Funktion ruft sich normalerweise ca. 2-mal rekursiv auf, der Resultierende Baum hat ungefähr Höhe \(n\) und somit ca \(2^n\) Knoten.
\(\rightarrow\) Zeit: \(O(2^n)\)
Der Baum wird "Depth First" traversiert, also ein Ast nach dem anderen, somit ist zu jedem Zeitpunkt höchstens ein Pfad von Wurzel bis Blatt im Speicher.
\(\rightarrow\) Speicher: \(O(n)\)
Speicher:
\(O(n)\)
Zeit:
\(O(2^n)\)
Komplexität
Speicherkomplexität
public static int fibo1(int n) {
if (n <= 1) return 1;
return fibo1(n - 1) + fibo1(n - 2);
}public static int fibo2(int n) {
if(n <= 1) return 1;
int[] memory = new int[n + 1];
memory[0] = 1;
memory[1] = 1;
for (int i = 2; i <= n; i++) {
memory[i] = memory[i - 1] + memory[i - 2];
}
return memory[n];
}public static int fibo3(int n) {
int last1 = 1;
int last2 = 1;
for (int i = 2; i <= n; i++) {
int temp = last1 + last2;
last1 = last2;
last2 = temp;
}
return last2;
}Speicher:
\(O(n)\)
Zeit:
\(O(2^n)\)
Zeit:
\(O(n)\)
Speicher:
\(O(n)\)
Speicher:
\(O(1)\)
Zeit:
\(O(n)\)
Pascal Schärli - PVK Informatik II 2021
Komplexität
Neue Problemgrösse bei mehr Zeit
- Wir haben ein Computer, welcher ein Problem mit \(O(f(n))\) der Grösse M in der Zeit t lösen kann.
- Was ist die lösbare Problemgrösse, falls wir k-Mal so viel Zeit zur Verfügung haben?
- Beispiel:
- Der Computer kann ein \(O(n^3)\) Problem kann in 10s einen Input der Grösse 1'000 verarbeiten
- Wie gross kann der Input sein, wenn man 20s zur Verfügung hat?
- Der Computer kann ein \(O(n^3)\) Problem kann in 10s einen Input der Grösse 1'000 verarbeiten
Pascal Schärli - PVK Informatik II 2021
Komplexität
Neue Problemgrösse bei mehr Zeit
- Komplexität \(O(n^3)\)
- Bisherige Inputgrösse 1'000
- Mehr Zeit: \(\times 2\)
- Der Computer macht ca \(1000^3 = 10^9\) Operationen in 10s
- In 20s Zeit kann er also \(2 \cdot 10^9\) Operationen machen
- Die neu bewältigbare Problemgrösse ist somit \(\sqrt[3]{2 \cdot 10^9} \approx 1260 \)
Pascal Schärli - PVK Informatik II 2021
Komplexität
Neue Problemgrösse bei mehr Zeit
- Komplexität \(O(f(n))\)
- Bisherige Inputgrösse \(M\)
- Mehr Zeit: \(\times k\)
- Der Computer macht ca \(f(M)\) Operationen
- Mit der zusätzlichen Zeit kann er also \(k \cdot f(M)\) Operationen machen
- Die neu bewältigbare Problemgrösse ist somit \(f^{-1}(k \cdot f(M))\)
Pascal Schärli - PVK Informatik II 2021
Herbst 2017, 0.67 Notenpunkte
Laufzeit und Speicherkomplexität
Prüfungsaufgabe
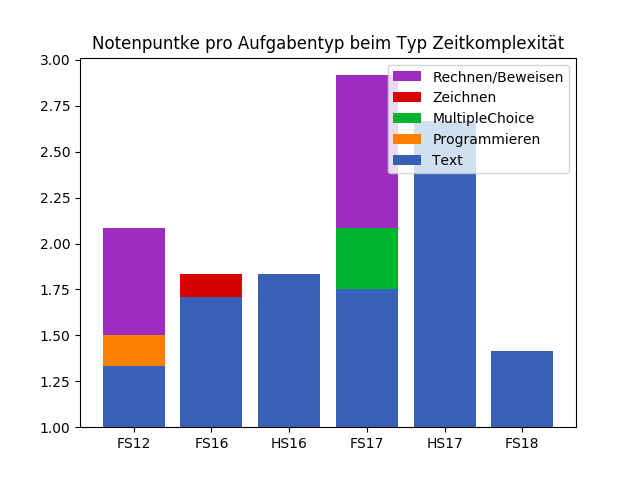
Pascal Schärli - PVK Informatik II 2021
Laufzeit und Speicherkomplexität
Prüfungsaufgabe
Herbst 2017, 0.67 Notenpunkte
public static int algorithm1(int[] input){
assert input != null && input.length > 0;
int maxSum = input[0];
for(int i = 0; i < input.length; i++){
for(int j = 0; j < input.length; j++){
int sum = 0;
for(int k = i; k <= j; k++){
sum += input[k];
}
if(sum > maxSum){
maxSum = sum;
}
}
}
return maxSum;
}Zeit:
\(O(input.length^3)\)
Zusätzlicher Speicher:
\(O(1)\)
Pascal Schärli - PVK Informatik II 2021
Laufzeit und Speicherkomplexität
Prüfungsaufgabe
Herbst 2017, 0.67 Notenpunkte
public static int algorithm2(int[] input){
assert input != null && input.length > 0;
// calculate partial sums
int[] p = new int[input.length];
for(int i = 0; i < input.length; i++){
if(i == 0) p[i] = input[i];
else p[i] = p[i-1] + input[i];
}
// search for the maximum partial sum
int maxSum = input[0];
for(int i = 0; i < input.length; i++){
for(int j = i; j < input.length; j++){
int sum = (i == j) ? p[j] : p[j] - p[i];
if(sum > maxSum){
maxSum = sum;
}
}
}
return maxSum;
}Zeit:
\(O(input.length^2)\)
Zusätzlicher Speicher:
\(O(input.length)\)
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Pascal Schärli - PVK Informatik II 2021
Array
Datenstrukturen
Konzept
- Speichert Liste von Elementen
- Daten sind Physisch im Speicher nacheinander gespeichert
Vorteile
- Konstante Zeit für Lesen/Schreiben
- Platzsparend
Wichtigste Operationen
- get - Element Lesen
- \(O(1)\)
- set - Element Schreiben
- \(O(1)\)
Nachteile
- Aufwendig Reihenfolge der Elemente zu verändern
- Fixe Grösse
Pascal Schärli - PVK Informatik II 2021
Linked List
Datenstrukturen
Konzept
- Speichert Liste von Elementen
- Reihenfolge ist nicht durch Physischen Speicherort gegeben
- Jedes Element hat einen Zeiger auf seinen Nachfolger
Vorteile
- Flexible Grösse
- Reihenfolge kann einfach verändert werden
Wichtigste Operationen
- get - Element Lesen
- \(O(n)\)
- set - Element Schreiben
- \(O(n)\)
- insert - Element Einfügen
- \(O(n)\)
Nachteile
- \(O(n)\) für Lesen/Schreiben
- Mehr Speicherplatz da jedes Element einen zusätzlichen Zeiger hat.
Pascal Schärli - PVK Informatik II 2021
Stack
Datenstrukturen
Konzept
- Elemente werden oben auf einen Stapel gelegt und von oben wieder weg genommen
- LIFO Last In First Out
Wichtigste Operationen
- push - Element auf Stapel Legen
- \(O(1)\) (mit Linked List)
- pop - Element von Stapel entfernen
- \(O(1)\) (mit Linked List)
- peek - Oberstes Element anschauen
- \(O(1)\) (mit Linked List)
Pascal Schärli - PVK Informatik II 2021
Queue
Datenstrukturen
Konzept
- Elemente werden hinten in eine Warteschlange getan und vorne wieder rausgenommen.
- FIFO First In First Out
Anwendungen
- Bei geteilten Ressourcen, z.B. Zeitplanungen für CPU, Festplatte
- Bei asynchronen Datenübertragung, also wenn bei einer Übertragung Daten nicht gleichzeitig bereitgestellt und verarbeitet werden.
Wichtigste Operationen
- enqueue - Element hinten in die Warteschlange setzen
- \(O(1)\) (mit Doubly Linked List)
- dequeue - Element vorne von der Warteschlange entfernen
- \(O(1)\) (mit Doubly Linked List)
Pascal Schärli - PVK Informatik II 2021
Graph
Datenstrukturen
Kanten
Knoten
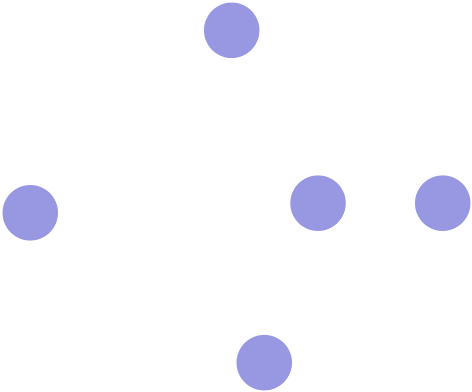
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadPascal Schärli - PVK Informatik II 2021
Graph
Datenstrukturen
Kanten haben eine Richtung
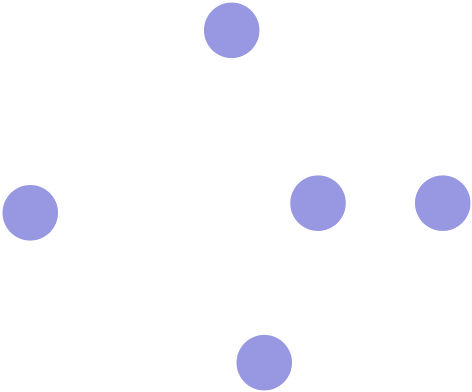
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadPascal Schärli - PVK Informatik II 2021
Graph
Datenstrukturen
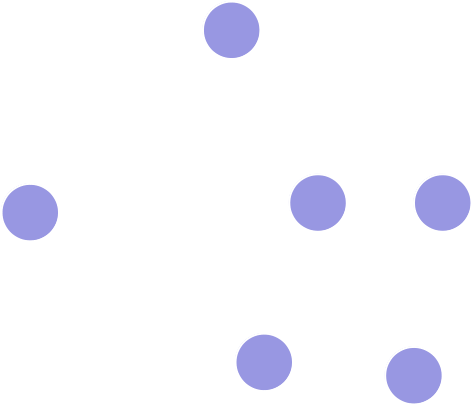
Zusammenhängender, Gerichteter Graph ohne Zyklen
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadPascal Schärli - PVK Informatik II 2021
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadKnoten ohne Kindknoten
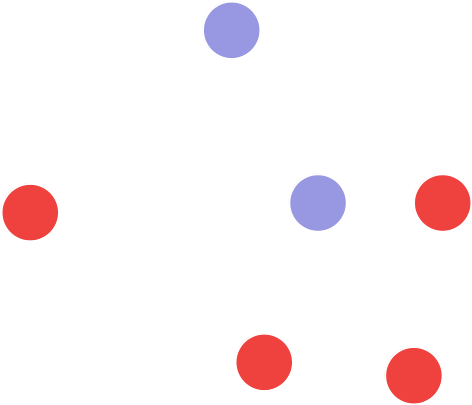
Datenstrukturen
Graph
Pascal Schärli - PVK Informatik II 2021
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
Pfadjeder Knoten besitzt höchstens zwei Kindknoten, die Reihenfolge der Kindknoten ist relevant.
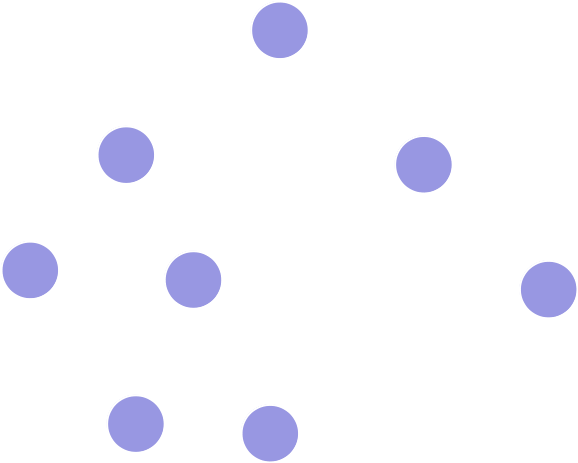
Datenstrukturen
Graph
Pascal Schärli - PVK Informatik II 2021
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
Pfadjeder Knoten besitzt entweder zwei oder keine Kinder
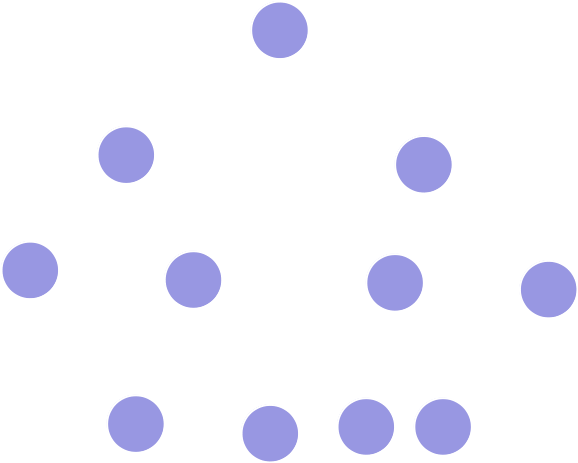
Datenstrukturen
Graph
Pascal Schärli - PVK Informatik II 2021
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadAlle Blätter haben die selbe Tiefe
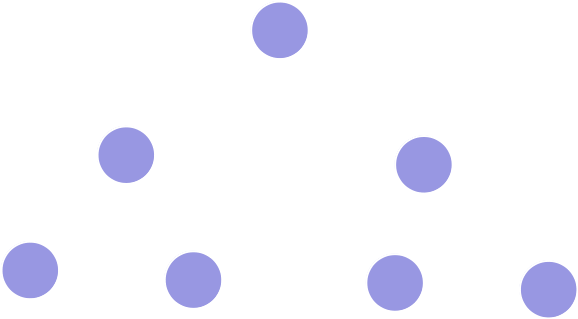
Datenstrukturen
Graph
Pascal Schärli - PVK Informatik II 2021
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadUngleich verteilter Baum

Datenstrukturen
Graph
Pascal Schärli - PVK Informatik II 2021
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadAnzahl “Levels” ohne Wurzel
→ hier: 3

Datenstrukturen
Graph
Pascal Schärli - PVK Informatik II 2021
Graph
Gerichteter Graph
Baum
Blätter
Binärbaum
Voller Baum
Vollständiger Baum
Entarteter Baum
Höhe
PfadWeg durch Graph (Nur in Pfeilrichtung)
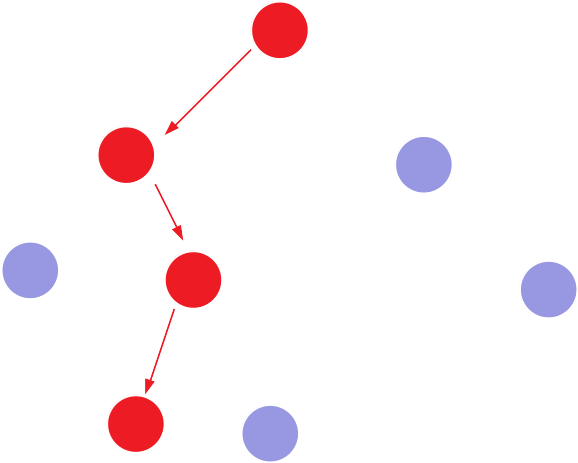
Datenstrukturen
Graph
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Pre-Order Traversierung
12 5 3 1 9 10 19 14 20 22
14
Gib den Wert vom Knoten aus
Gib den linken Teilbaum in Pre-Order aus
Gib den rechten Teilbaum in Pre-Order aus22
20
19
12
10
9
5
3
1
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
In-Order Traversierung
1 3 5 9 10 12 14 19 20 22
14
Gib den linken Teilbaum in In-Order aus
Gib den Wert vom Knoten aus
Gib den rechten Teilbaum in In-Order aus22
20
19
12
10
9
5
3
1
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Post-Order Traversierung
1 3 10 9 5 14 22 20 19 12
14
Gib den linken Teilbaum in Post-Order aus
Gib den rechten Teilbaum in Post-Order aus
Gib den Wert vom Knoten aus22
20
19
12
10
9
5
3
1
Pascal Schärli - PVK Informatik II 2021
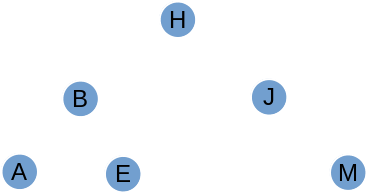
[ , , , , , , ]
Datenstrukturen
Binärbäume
- Binärbäume kann man in einem Array abspeichern
- Man muss ein Symbol für leere Knoten abmachen, z.B. ' '
- Mit den folgenden Formeln kann man den Baum traversieren:
-
left child: 2*i+1
-
right child: 2*i+2
-
parent: ⌊(i-1)/2⌋
-
'H'
0
'B '
1
'J'
2
'A '
3
'E'
4
' '
5
'M'
6
0
1
3
4
5
6
2
Pascal Schärli - PVK Informatik II 2021
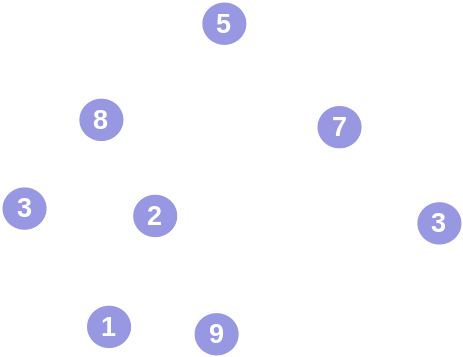
Indent = 1
Indent = 2
Indent = 3
Indent = 0
5
5
.8
5
.8
..3
5
.8
..3
..25
.8
..3
..2
...15
.8
..3
..2
...1
...95
.8
..3
..2
...1
...9
.75
.8
..3
..2
...1
...9
.7
..35
8
3
2
1
9
7
3
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binärbäume

5( )5(8( ) )5(8(3 ) )5(8(3,2( )) )5(8(3,2(1 )) )5(8(3,2(1,9)) )5(8(3,2(1,9)),7( ))5(8(3,2(1,9)),7(3))Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binärbäume

5
8
7
3
2
9
3
1
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binärbäume
1
3
5
6
9
10
12
18
20
19
22
- Alle Elemente im linken Ast sind kleiner
- Alle Elemente im rechten Ast sind grösser
- \(\rightarrow\) kleinstes Element ganz links
- \(\rightarrow\) grösstes Element ganz rechts
Binäre Suchbäume
Datenstrukturen
Pascal Schärli - PVK Informatik II 2021
1
3
5
6
9
10
12
18
20
19
22
Gesucht: 9
Datenstrukturen
Element Finden
- Falls der Knoten das gesuchte Element ist:
\(\rightarrow\) gefunden!
- Falls der gesuchte Wert kleiner als der Knoten ist:
\(\rightarrow\) Links weitersuchen
- Falls der gesuchte Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts weitersuchen
Pascal Schärli - PVK Informatik II 2021
Binäre Suchbäume
1
3
5
6
9
10
12
18
20
19
22
Gesucht: 9
Element Finden
- Falls der Knoten das gesuchte Element ist:
\(\rightarrow\) gefunden!
-
Falls der gesuchte Wert kleiner als der Knoten ist:
\(\rightarrow\) Links weitersuchen
- Falls der gesuchte Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts weitersuchen
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binäre Suchbäume
1
3
5
6
9
10
12
18
20
19
22
Gesucht: 9
Element Finden
- Falls der Knoten das gesuchte Element ist:
\(\rightarrow\) gefunden!
- Falls der gesuchte Wert kleiner als der Knoten ist:
\(\rightarrow\) Links weitersuchen
- Falls der gesuchte Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts weitersuchen
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binäre Suchbäume
1
3
5
6
9
10
12
18
20
19
22
Gesucht: 9
Element Finden
-
Falls der Knoten das gesuchte Element ist:
\(\rightarrow\) gefunden!
- Falls der gesuchte Wert kleiner als der Knoten ist:
\(\rightarrow\) Links weitersuchen
- Falls der gesuchte Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts weitersuchen
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binäre Suchbäume
1
3
5
6
9
10
12
18
20
19
22
Gesucht: 15
Element Finden
- Falls der Knoten das gesuchte Element ist:
\(\rightarrow\) gefunden!
- Falls der gesuchte Wert kleiner als der Knoten ist:
\(\rightarrow\) Links weitersuchen
- Falls der gesuchte Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts weitersuchen
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binäre Suchbäume
1
3
5
6
9
10
12
18
20
19
22
Gesucht: 15
Element Finden
- Falls der Knoten das gesuchte Element ist:
\(\rightarrow\) gefunden!
-
Falls der gesuchte Wert kleiner als der Knoten ist:
\(\rightarrow\) Links weitersuchen
- Falls der gesuchte Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts weitersuchen
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
Binäre Suchbäume
1
3
5
6
9
10
12
18
20
19
22
\(\rightarrow\) Nicht vorhanden
Binäre Suchbäume
Gesucht: 15
Element Finden
- Falls der Knoten das gesuchte Element ist:
\(\rightarrow\) gefunden!
- Falls der gesuchte Wert kleiner als der Knoten ist:
\(\rightarrow\) Links weitersuchen
- Falls der gesuchte Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts weitersuchen
Pascal Schärli - PVK Informatik II 2021
Datenstrukturen
1
3
5
6
9
10
12
18
20
19
22
14
Binäre Suchbäume
Datenstrukturen
Element Einfügen
- Falls der Knoten leer ist
\(\rightarrow\) fertig!
- Falls der einzufügende Wert kleiner als der Knoten ist:
\(\rightarrow\) Links einfügen
- Falls der einzufügende Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts einfügen
Pascal Schärli - PVK Informatik II 2021
1
3
5
6
9
10
12
18
20
19
22
14
Binäre Suchbäume
Datenstrukturen
Pascal Schärli - PVK Informatik II 2021
Element Einfügen
- Falls der Knoten leer ist
\(\rightarrow\) fertig!
-
Falls der einzufügende Wert kleiner als der Knoten ist:
\(\rightarrow\) Links einfügen
- Falls der einzufügende Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts einfügen
1
3
5
6
9
10
12
18
20
19
22
14
Pascal Schärli - PVK Informatik II 2021
Element Einfügen
-
Falls der Knoten leer ist
\(\rightarrow\) fertig!
- Falls der einzufügende Wert kleiner als der Knoten ist:
\(\rightarrow\) Links einfügen
- Falls der einzufügende Wert grösser als der Knoten ist:
\(\rightarrow\) Rechts einfügen
Binäre Suchbäume
Datenstrukturen
1
3
5
6
9
10
12
18
20
19
22
14
Element Entfernen
-
Methode 1:
- Ersetzen durch kleinstes Element im rechten Teilbaum
- Methode 2:
- Ersetzen durch grösstes Element im linken Teilbaum
Pascal Schärli - PVK Informatik II 2021
Binäre Suchbäume
Datenstrukturen
1
3
5
6
9
10
12
20
22
19
14
Pascal Schärli - PVK Informatik II 2021
Element Entfernen
-
Methode 1:
- Ersetzen durch kleinstes Element im rechten Teilbaum
- Methode 2:
- Ersetzen durch grösstes Element im linken Teilbaum
Binäre Suchbäume
Datenstrukturen
1
3
5
6
9
10
12
19
20
22
14
Element Entfernen
- Methode 1:
- Ersetzen durch kleinstes Element im rechten Teilbaum
-
Methode 2:
- Ersetzen durch grösstes Element im linken Teilbaum
Binäre Suchbäume
Datenstrukturen
Pascal Schärli - PVK Informatik II 2021
1
3
5
9
10
12
20
22
19
14
Element Entfernen
- Methode 1:
- Ersetzen durch kleinstes Element im rechten Teilbaum
-
Methode 2:
- Ersetzen durch grösstes Element im linken Teilbaum
Binäre Suchbäume
Datenstrukturen
Pascal Schärli - PVK Informatik II 2021
Laufzeiten
- Die Laufzeit der Operationen ist abhängig von der Höhe vom Baum.
- Falls der Baum entartet ist, ist die Höhe grösser und somit die Laufzeit schlechter.
- Die Operationen "Element Finden", "Element Einfügen" und "Element Löschen" haben alle die selbe Laufzeit:
- Best&Average case: \(O(log(n))\)
- Worst case: \(O(n)\)
Binäre Suchbäume
Datenstrukturen
Pascal Schärli - PVK Informatik II 2021
Heaps
Datenstrukturen
6
11
5
3
2
- Um dem Problem von entarteten Binären Suchbäumen entgegenzuwirken benutzen wir Heaps.
- Ein Heap ist ein Binärbaum mit den folgenden Eigenschaften:
- Alle bis auf die letzte Ebene sind vollständig besetzt
- Die letzte Ebene wird von rechts nach links aufgefüllt
- Die Elemente sind geordnet:
- Max-Heap: Alle Kinder sind kleiner als die Wurzel
- Min-Heap: Alle Kinder sind grösser als die Wurzel
Pascal Schärli - PVK Informatik II 2021
Element Einfügen
- Um ein Element einzufügen, fügt man es in der Untersten Ebene beim ersten freien Platz ein.
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird das Element so lange mit seinem Vorgänger getauscht, bis es grösser als sein Vorgänger ist.
2
5
8
4
3
9
12
6
11
7
5
4
1
Datenstrukturen
Heaps
Pascal Schärli - PVK Informatik II 2021
Element Einfügen
- Um ein Element einzufügen, fügt man es in der Untersten Ebene beim ersten freien Platz ein.
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird das Element so lange mit seinem Vorgänger getauscht, bis es grösser als sein Vorgänger ist.
2
5
8
4
3
9
12
6
11
7
5
4
1
Datenstrukturen
Heaps
Pascal Schärli - PVK Informatik II 2021
Element Einfügen
- Um ein Element einzufügen, fügt man es in der Untersten Ebene beim ersten freien Platz ein.
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird das Element so lange mit seinem Vorgänger getauscht, bis es grösser als sein Vorgänger ist.
2
5
8
4
3
9
12
6
11
7
5
4
1
Datenstrukturen
Heaps
Pascal Schärli - PVK Informatik II 2021
Wurzel Entfernen
- Um die Wurzel zu entfernen ersetzt man die Wurzel mit dem Letzten Element im Stack
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird die neue Wurzel so lange mit seinem kleinsten Kind getauscht, bis es kleiner als alle Kinder ist.
4
5
8
3
2
9
12
6
11
7
5
4
1
Pascal Schärli - PVK Informatik II 2021
Heaps
Datenstrukturen
Wurzel Entfernen
- Um die Wurzel zu entfernen ersetzt man die Wurzel mit dem Letzten Element im Stack
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird die neue Wurzel so lange mit seinem kleinsten Kind getauscht, bis es kleiner als alle Kinder ist.
4
5
8
3
2
9
12
6
11
7
5
4
1
Pascal Schärli - PVK Informatik II 2021
Heaps
Datenstrukturen
4
5
8
3
2
9
12
6
11
7
5
4
1
Pascal Schärli - PVK Informatik II 2021
Heaps
Datenstrukturen
Wurzel Entfernen
- Um die Wurzel zu entfernen ersetzt man die Wurzel mit dem Letzten Element im Stack
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird die neue Wurzel so lange mit seinem kleinsten Kind getauscht, bis es kleiner als alle Kinder ist.
4
5
8
3
2
9
12
6
11
7
5
4
Pascal Schärli - PVK Informatik II 2021
Heaps
Datenstrukturen
Wurzel Entfernen
- Um die Wurzel zu entfernen ersetzt man die Wurzel mit dem Letzten Element im Stack
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird die neue Wurzel so lange mit seinem kleinsten Kind getauscht, bis es kleiner als alle Kinder ist.
4
5
8
3
2
9
12
6
11
7
5
4
Pascal Schärli - PVK Informatik II 2021
Heaps
Datenstrukturen
Wurzel Entfernen
- Um die Wurzel zu entfernen ersetzt man die Wurzel mit dem Letzten Element im Stack
- Dies könnte in einem ungültigen Heap resultieren
- Deshalb wird die neue Wurzel so lange mit seinem kleinsten Kind getauscht, bis es kleiner als alle Kinder ist.
Frühling 2016, 0.67 Notenpunkte
Bäume
Prüfungsaufgabe
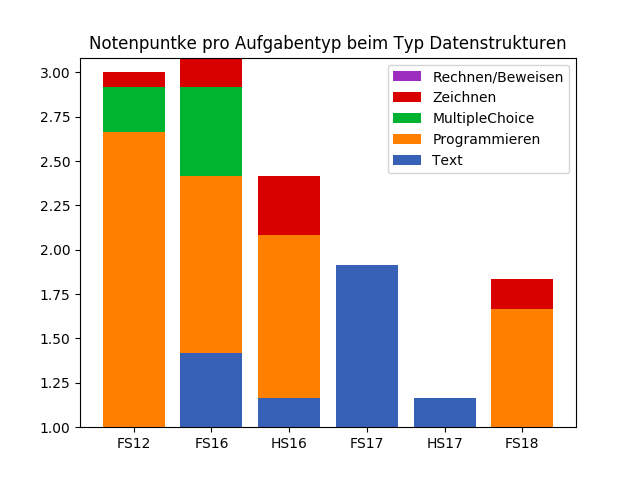
Pascal Schärli - PVK Informatik II 2021
Bäume
Prüfungsaufgabe
Frühling 2016, 0.67 Notenpunkte
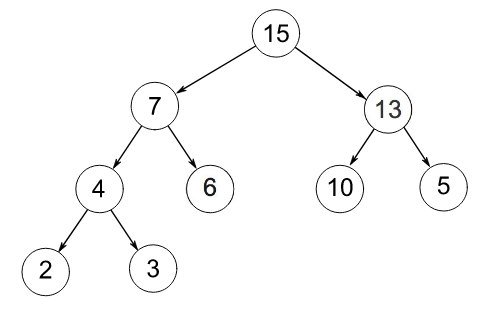
- Der Baum ist ein Binärbaum
- Er ist kein Binärer Suchbaum
- Er ist ein (Max-)Heap
- Es gibt nichtleere Heaps, welche Suchbäume sind
- Jeder (Such-)Baum mit n>0 Knoten hat n-1 Kanten
- Die Inorder Traversierung von einem Binären Suchbaum gibt immer eine sortierte Folge
Inorder Traversierung:
2 4 3 7 6 15 10 13 5
Pascal Schärli - PVK Informatik II 2021
Bäume
Prüfungsaufgabe
Frühling 2016, 0.67 Notenpunkte
- Minimale Knotenzahl eines binären Suchbaums der Höhe \(h\)
- \(h+1\) (Baum mit 1 Knoten hat Höhe 0)
- Maximale Knotenzahl bei Max-Heap der Höhe \(h\)
- \(2^{h+1}-1\)
- Elemente in dieser Reihenfolge eingefügt: 4 – 5 – 8 – 1 – 2 – 3 – 7 – 0
4
5
8
1
2
3
7
0
Pascal Schärli - PVK Informatik II 2021
Java Bytecode
Pascal Schärli - PVK Informatik II 2021
Motivation
Java Bytecode
- Java funktioniert cross-plattform auf unterschiedlichsten Gerätetypen und Architekturen.
- Um die selbe Funktionalität für all diese Geräte zu ermöglichen, gibt es beim Kompilieren eine Zwischenstufe, der Bytecode.
- Dieser kann dann für die jeweilige Architektur in Maschinensprache übersetzt werden.
- Auf Wikipedia gibt es eine Liste von allen Bytecode Instruktionen.
Pascal Schärli - PVK Informatik II 2021
Operand Stack
Java Bytecode
Stack
Bytecode
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iadd- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
Pascal Schärli - PVK Informatik II 2021
- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iaddBytecode
Stack
4
Java Bytecode
Operand Stack
Pascal Schärli - PVK Informatik II 2021
- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iaddBytecode
Stack
4
2
Java Bytecode
Operand Stack
Pascal Schärli - PVK Informatik II 2021
- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iaddBytecode
Stack
4
2
3
Java Bytecode
Operand Stack
Pascal Schärli - PVK Informatik II 2021
- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iaddBytecode
Stack
4
6
Java Bytecode
Operand Stack
Pascal Schärli - PVK Informatik II 2021
- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iaddBytecode
Stack
4
6
1
Java Bytecode
Operand Stack
Pascal Schärli - PVK Informatik II 2021
- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iaddBytecode
Stack
4
5
Java Bytecode
Operand Stack
Pascal Schärli - PVK Informatik II 2021
- Der Bytecode arbeitet mit einem "Operand Stack"
- Die Werte mit welchen gerechnet wird, befinden sich auf einem Stack und wir verarbeiten immer die obersten Elemente auf dem Stack.
iconst_4
iconst_2
iconst_3
imul
iconst_1
isub
iaddBytecode
Stack
9
Java Bytecode
Operand Stack
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
}Bytecode
Übersetzung
Stack
a
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
a
}Bytecode
Übersetzung
Stack
a
1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
a 1
}Bytecode
Übersetzung
Stack
a
1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
}
}Bytecode
Übersetzung
Stack
a
1
a > 1
1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
1
}
}Bytecode
Übersetzung
Stack
1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
}Bytecode
Übersetzung
Stack
1
1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
a
}Bytecode
Übersetzung
Stack
a
1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
a 1
}Bytecode
Übersetzung
Stack
a
1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
a-1
}Bytecode
Übersetzung
Stack
a
1
a-1
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
f(a-1)
}Bytecode
Übersetzung
Stack
a
1
f(a-1)
a
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
f(a-1) a
}Bytecode
Übersetzung
Stack
a
1
f(a-1)
a
2
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
f(a-1) a 2
}Bytecode
Übersetzung
Stack
a
1
f(a-1)
a
2
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
f(a-1) a-2
}Bytecode
Übersetzung
Stack
a
1
f(a-1)
a
2
a-2
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
f(a-1) f(a-2)
}Bytecode
Übersetzung
Stack
a
1
f(a-1)
f(a-2)
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
f(a-1) + f(a-2)
}Bytecode
Übersetzung
Stack
a
1
f(a-1)
f(a-2)
f(a-1) + f(a-2)
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
return f(a-1) + f(a-2);
}Bytecode
Übersetzung
Stack
a
1
f(a-1)
f(a-2)
f(a-1) + f(a-2)
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
static int f(int a);
0 iload_0 [a]
1 iconst_1
2 if_icmpgt 7
5 iconst_1
6 ireturn
7 iload_0 [a]
8 iconst_1
9 isub
10 invokestatic test.Main.f(int) : int [16]
13 iload_0 [a]
14 iconst_2
15 isub
16 invokestatic test.Main.f(int) : int [16]
19 iadd
20 ireturnstatic int f(int a) {
if(a <= 1){
return 1;
}
return f(a-1) + f(a-2);
}Bytecode
Übersetzung
Stack
Java Bytecode
Bytecode Verstehen
Pascal Schärli - PVK Informatik II 2021
Herbst 2017, 0.34 Notenpunkte
Bytecode
Prüfungsaufgabe
Pascal Schärli - PVK Informatik II 2021
Bytecode
Prüfungsaufgabe
Herbst 2017, 0.34 Notenpunkte
public class IncrementingInteger{
public static void main(){
System.out.println(expr1(1));
System.out.println(expr2(1));
}
public static int expr1(int value){
int x = (value++)*2;
return x;
}
public static int expr2(int value){
int x = (++value)*2;
return x;
}
}2
4Code A:
0: iload_0
1: iinc 0, 1
2: iconst_2
3: imul
4: istore_1
5: iload_1
6: ireturnCode B:
0: iinc 0, 1
1: iload_0
2: iconst_2
3: imul
4: istore_1
5: iload_1
6: ireturnexpr1expr2Pascal Schärli - PVK Informatik II 2021
Algorithmen

Pascal Schärli - PVK Informatik II 2021
Altägyptische Multiplikation
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Altägyptische Multiplikation
1
3
6
12
24
49
98
320
160
80
40
20
10
5
f(5,98) = 320 + 160 + 10 = 490
f(320,1) = 320
f(160,3) = f(320,1) + 160
f(80,6) = f(160,3)
f(40,12) = f(80,6)
f(20,24) = f(40,12)
f(10,49) = f(20,24) + 10
f(5,98) = f(10,49)
| a | b | f(a,b) |
|---|---|---|
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Altägyptische Multiplikation
\(f(a,n) = f(2a,\frac{n-1}{2}) + a\)
\(\frac{n-1}{2} \in [1 \ldots n-1]\)
\(f(2a,\frac{n-1}{2}) + a=2a \cdot \frac{n-1}{2} + a\)
\(=a \cdot n \)
\(n\) ungerade:
\(f(a,n) = f(2a,\frac{n}{2})\)
\(\frac{n}{2} \in [1 \ldots n-1]\)
\(f(2a,\frac{n}{2})=2a \cdot \frac{n}{2}\)
\(=a \cdot n \)
\(n\) gerade:
Gegeben, dass \(f(a,b) = a \cdot b \) für \(b \in [1 \dots n-1] \).
Zeige daraus, dass \(f(a,n) = a \cdot n\).
Induktionsschritt:
Induktionsverankerung: \(b = 1 \)
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Ackermann
- Die Ackermannfunktion ist eine extrem schnell wachsende Funktion, mit deren Hilfe in der theoretischen Informatik Grenzen von Modellen aufgezeigt werden können.
- Rekursive Definition:
- \(A(0,m) = m + 1\)
- \(A(n,0) = A(n-1,1)\)
- \(A(n,m) = A(n-1,A(n,m-1))\)
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Ackermann
Weitere Beispiele:
\(A(0,m) = m + 1\)
\(A(n,0) = A(n-1,1)\)
\(A(n,m) = A(n-1,A(n,m-1))\)
\(2^{65536} - 3 \)
\(65533\)
\(13\)
- \(A(4,0) = \)
- \(A(4,1) = \)
- \(A(4,2) = \)
\(\Rightarrow A(1,1) = 3\)
A(1,1) // A(1,1)
A(1,0) // A(1,1) = A(0,A(1,0))
A(0, 1) // A(1,0) = A(0,1)
<- 2 // A(0,1) = 2
<- 2 // A(1,0) = 2
A(0, 2) // A(1,1) = A(0,2)
<- 3 // A(0,2) = 3
<- 3 // A(1,1) = 3
A(1,1) // A(1,1)
A(1,0) // A(1,1) = A(0,A(1,0))
A(0, 1) // A(1,0) = A(0,1)
<- 2 // A(0,1) = 2
<- 2 // A(1,0) = 2
A(0, 2) // A(1,1) = A(0,2)
<- 3 // A(0,2) = 3
A(1,1) // A(1,1)
A(1,0) // A(1,1) = A(0,A(1,0))
A(0, 1) // A(1,0) = A(0,1)
<- 2 // A(0,1) = 2
<- 2 // A(1,0) = 2
A(0, 2) // A(1,1) = A(0,2)
A(1,1) // A(1,1)
A(1,0) // A(1,1) = A(0,A(1,0))
A(0, 1) // A(1,0) = A(0,1)
<- 2 // A(0,1) = 2
<- 2 // A(1,0) = 2
A(1,1) // A(1,1)
A(1,0) // A(1,1) = A(0,A(1,0))
A(0, 1) // A(1,0) = A(0,1)
<- 2 // A(0,1) = 2
A(1,1) // A(1,1)
A(1,0) // A(1,1) = A(0,A(1,0))
A(0, 1) // A(1,0) = A(0,1)
A(1,1) // A(1,1)
A(1,0) // A(1,1) = A(0,A(1,0))
A(1,1) // A(1,1)
Beispiel: \(A(1,1)\)
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Binäre Suche
- Gegeben wird ein sortierter Array [1,2,4,6,9,10,14,16,17,20,23,26]
- Welcher Index hat 16?
- Alle Elemente durchprobieren.
\(\rightarrow\) nicht sehr effizient
- Eventuell kann man ausnutzen, dass der Array bereits sortiert ist?
\(\rightarrow\) Binäre Suche!
- Alle Elemente durchprobieren.
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Binäre Suche:
Gesuchter Wert mit der Mitte/Pivot vergleichen.
Gleich wie die Mitte?
-> Gefunden!
Grösser als die Mitte?
-> rechts weitersuchen
Kleiner als die Mitte?
-> links weitersuchen26
1
2
4
6
9
10
14
16
17
20
23
11
0
1
2
3
4
5
6
7
8
9
10
pivot
10
Vergleich:
16
?
>
Binäre Suche
Algorithmen
Pascal Schärli - PVK Informatik II 2021
11
0
1
2
3
4
5
6
7
8
9
10
17
Vergleich:
16
?
<
Binäre Suche
Binäre Suche:
Gesuchter Wert mit der Mitte/Pivot vergleichen.
Gleich wie die Mitte?
-> Gefunden!
Grösser als die Mitte?
-> rechts weitersuchen
Kleiner als die Mitte?
-> links weitersuchenpivot
23
20
17
16
14
10
9
6
4
2
1
26
Algorithmen
Pascal Schärli - PVK Informatik II 2021
14
Vergleich:
16
?
>
Binäre Suche
Binäre Suche:
Gesuchter Wert mit der Mitte/Pivot vergleichen.
Gleich wie die Mitte?
-> Gefunden!
Grösser als die Mitte?
-> rechts weitersuchen
Kleiner als die Mitte?
-> links weitersuchenpivot
23
20
17
16
14
10
9
6
4
2
1
26
Algorithmen
11
0
1
2
3
4
5
6
7
8
9
10
Pascal Schärli - PVK Informatik II 2021
16
Vergleich:
16
?
=
Binäre Suche
pivot
23
20
17
16
14
10
9
6
4
2
1
26
Binäre Suche:
Gesuchter Wert mit der Mitte/Pivot vergleichen.
Gleich wie die Mitte?
-> Gefunden!
Grösser als die Mitte?
-> rechts weitersuchen
Kleiner als die Mitte?
-> links weitersuchenAlgorithmen
11
0
1
2
3
4
5
6
7
8
9
10
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z
- Gleiches Konzept wie BNF
- Ein Ausdruck ist erzeugbar, wenn es einen Weg durch das Diagramm gibt, welcher diesen beschreibt
Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z









A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z









A(B(C,D))


Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z
A(B(C,D))











Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z
A(B(C,D))











Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z
A(B(C,D))











Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z
A(B(C,D))











Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z
A(B(C,D))











Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z











A(B(C,D))
Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z











A(B(C,D))
Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z










A(B(C,D))

Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z









A(B(C,D))


Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z








A(B(C,D))



Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z







A(B(C,D))




Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z






A(B(C,D))





Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z






A(B(C,D))





Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z






A(B(C,D))





Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z






A(B(C,D))





Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z





A(B(C,D))






Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z





A(B(C,D))






Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z





A(B(C,D))






Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z





A(B(C,D))






Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z




A(B(C,D))







Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z




A(B(C,D))







Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z




A(B(C,D))







Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z




A(B(C,D))







Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z




A(B(C,D))







Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z




A(B(C,D))







Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z



A(B(C,D))








Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z



A(B(C,D))








Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z



A(B(C,D))








Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z



A(B(C,D))








Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z



A(B(C,D))








Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z



A(B(C,D))








Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z



A(B(C,D))








Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z


A(B(C,D))









Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z


A(B(C,D))









Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z


A(B(C,D))









Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z


A(B(C,D))









Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z


A(B(C,D))










Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Knoten
Unterbäume
Baum
(
)
Baum
Unterbäume
,
Knoten
B
A
C
Z


A(B(C,D))










Parser
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Algorithmen
+
)
(
Clause
Var
neuen offset zurückgeben
parst ')'
sonst offset erhöhen ('+' parsen)
falls kein '+' folgt, Schleife abbrechen
parst Var
parst '('
private static int parseClause(String kd, int offset) throws ParseException {
if (!checkNext('(', kd, offset)) {
throw new ParseException("expected '('", offset);
}
offset++;
while(true){
offset = parseVar(kd, offset);
if (!checkNext('+', kd, offset)) {
break;
}
offset++;
}
if (!checkNext(')', kd, offset)) {
throw new ParseException("expected ')'", offset);
}
offset++;
return offset;
}Parser
Pascal Schärli - PVK Informatik II 2021
Divide and Conquer
Algorithmen
- Komplexe Probleme können auf einfache Teilprobleme reduziert werden
- Diese Teilprobleme kann man weiter unterteilen, bis das Problem simpel genug ist
-
Teile und Herrsche
- Beispiele:
- Türme von Hanoi
- Mergesort
Pascal Schärli - PVK Informatik II 2021
Merge-Sort
Algorithmen
3
2
1
1
4
7
2
5
6
8
3
1
4
7
2
5
6
8
3
8
7
6
5
4
3
2
1
1
4
7
2
5
6
8
3
- Mergesort ist ein Sortieralgorithmus, durch divide and conquer funktioniert.
- Teile die Liste in zwei halb so grosse Listen auf
- Sortiere die halb so grossen Listen
- Verbinde die beiden sortierten Listen zu einer einzigen sortierten Liste
- Mergesort hat die Kompexität \(O(n \cdot log(n) \)
Pascal Schärli - PVK Informatik II 2021
Merge-Sort
Algorithmen

- Im Punkt 2 können wir die kleinen Teillisten wieder mit Mergesort sortieren
- Dies wiederholen wir, bis die Liste nur noch ein Element beinhaltet
3
2
1
1
4
7
2
5
6
8
3
1
4
7
2
5
6
8
3
8
7
6
5
4
3
2
1
1
4
7
2
5
6
8
3
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
1
2
4
7
ptr1
ptr2
3
8
6
5
1
2
4
7
3
8
6
5
Um zwei Listen zu Mergen kann man:
• einen Zeiger auf den Anfang von beiden Teillisten setzen
• Das kleinere Element dem Resultat hinzufügen und diesen Zeiger vergrössern
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
3
8
6
5
3
8
3
8
6
5
5
6
3
5
6
8
2
7
4
1
2
7
2
7
4
1
1
4
1
2
4
7
3
8
6
5
2
7
4
1
3
8
6
5
2
7
4
1
Merge-Sort
Algorithmen
Pascal Schärli - PVK Informatik II 2021
Algorithmen
Heap-Sort
-
Es ist möglich mit Heaps einen Array in-place zu sortieren, also ohne zusätzlichen Speicherplatz zu verwenden.
-
Dabei nutzen wir die Array-Darstellung von Binärbäumen.
-
Der Algorithmus läuft in zwei Phasen:
-
Zuerst erstellen wir eine Heapstruktur im Array
-
Danach können wir immer das grösste bzw kleinste Element aus dem Heap entfernen
-
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
9
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
unstrukturiert
im heap
sortiert
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
1
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
1
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
2
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
3
9
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
9
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
7
9
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
9
7
3
9
1
2
min heap (nur als visualisierung vom Array)
unstrukturiert
im heap
sortiert
Algorithmen
Heap-Sort
Pascal Schärli - PVK Informatik II 2021
- In Informatik I musstet ihr einen Sudoku-Solver Programmieren
- Die einfachste Lösung wäre alle möglichen Zahlenkombinationen auszuprobieren.
- Code ist kurz und überschaubar
- Die Laufzeit ist dafür unmenschlich lange
- Darum habt also nur Positionen geprüft, welche die Sudoku Regeln nicht verletzen.
- Code ist komplexer
- Die Laufzeit war jedoch viel schneller.
Backtracking
Algorithmen
Pascal Schärli - PVK Informatik II 2021
- Ein Dieb ist in ein Haus eingebrochen
- Der Dieb kennt von jedem Gegenstand dessen Wert \(v_i \geq 0\) sowie dessen Gewicht \(g_i \geq 0\).
- Er hat eine Tasche, in welche ein Gewicht \(G\) passt.
- Welche der Gegenstände \(x_1, ...., x_K\) soll er einpacken um den Wert der Beute zu maximieren.
Algorithmen
Backtracking
Pascal Schärli - PVK Informatik II 2021
000
001
010
011
100
101
110
111
0kg
0.-
2kg
200.-
1kg
50.-
3kg
250.-
4kg
100.-
6kg
300.-
5kg
150.-
7kg
350.-
00X
0kg
0.-
01X
1kg
50.-
10X
4kg
100.-
11X
5kg
150.-
0XX
0kg
0.-
1XX
4kg
100.-
XXX
0kg
0.-
Kapazität: 3kg
Alter Laptop: 4kg, 100.-
Michaels: 1kg, 50.-
Katze: 2kg, 200.-
Algorithmen
Backtracking
Pascal Schärli - PVK Informatik II 2021
000
001
010
011
100
101
110
111
0kg
0.-
2kg
200.-
1kg
50.-
3kg
250.-
4kg
100.-
6kg
300.-
5kg
150.-
7kg
350.-
Zu schwer
Beste Lösung:
Michaels & Katze mit Wert 250.-
Backtracking
Algorithmen
Katze: 2kg, 200.-
Michaels: 1kg, 50.-
Alter Laptop: 4kg, 100.-
Kapazität: 3kg
Pascal Schärli - PVK Informatik II 2021
000
001
010
011
0kg
0.-
2kg
200.-
1kg
50.-
3kg
250.-
00X
0kg
0.-
01X
1kg
50.-
0XX
0kg
0.-
1XX
4kg
100.-
XXX
0kg
0.-
Zu schwer
Viel Arbeit erspart
Backtracking
Algorithmen
Katze: 2kg, 200.-
Michaels: 1kg, 50.-
Alter Laptop: 4kg, 100.-
Kapazität: 3kg
Sobald wir wissen, dass der Zustand illegal ist, können wir zurück gehen und müssen dort nicht mehr weiterrechnen.
Pascal Schärli - PVK Informatik II 2021
Pascal Schärli - PVK Informatik II 2020
Frühling 2016, 0.35 Notenpunkte
Syntaxdiagramme
Prüfungsaufgabe
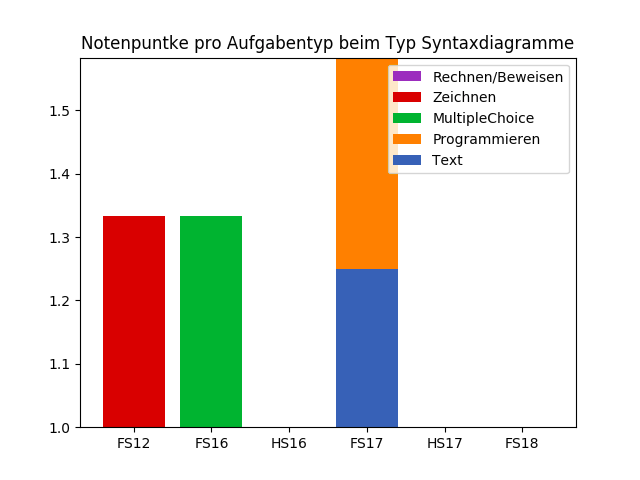
Pascal Schärli - PVK Informatik II 2021
Syntaxdiagramme
Prüfungsaufgabe
Frühling 2016, 0.35 Notenpunkte
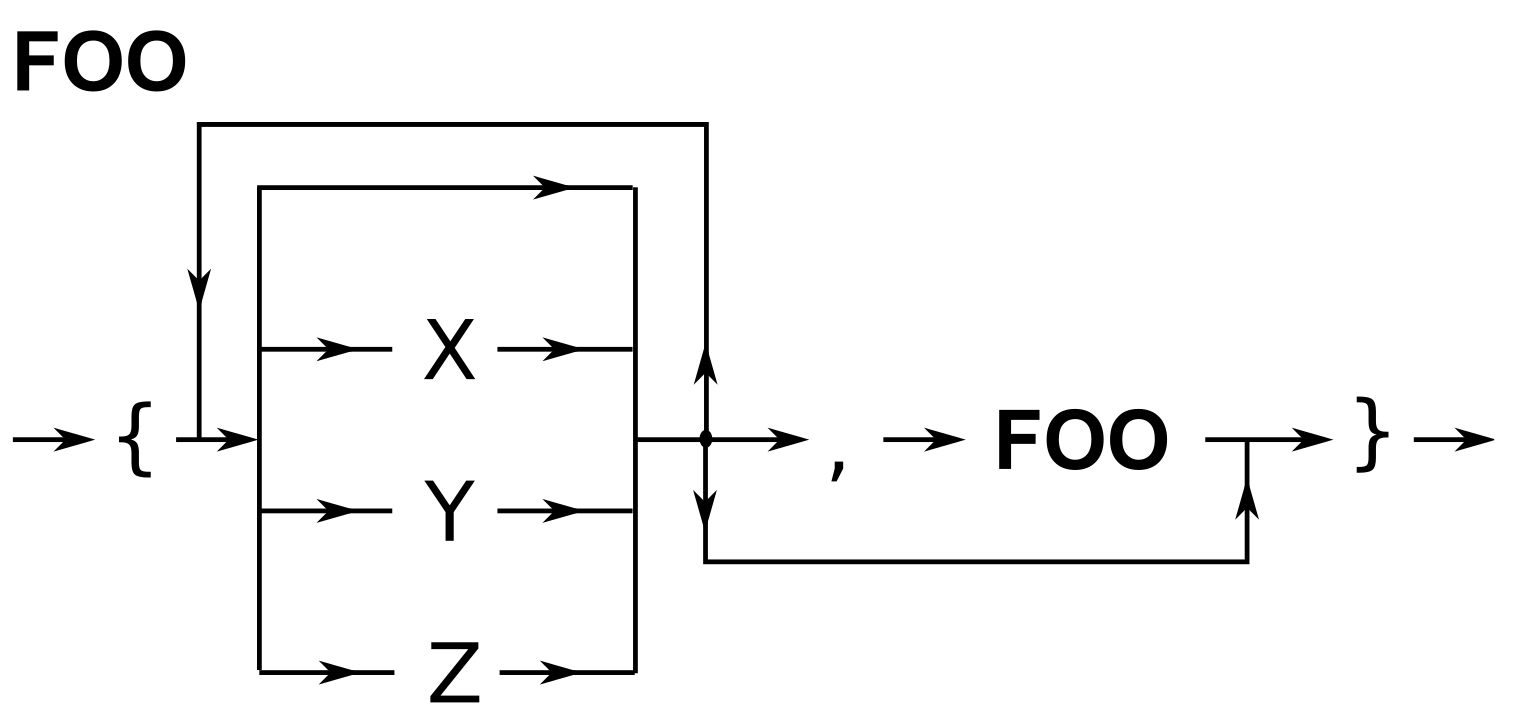
-
{XYZ} -
{X{Y{Z}}} -
{X,Y,{Z}} -
XYZ}
-
{XYZ -
{ -
{} -
{XY,{}}
Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung

Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Prozesse VS Threads
- Wenn man verschiedene Tasks parallel Ausführt, kann die Laufzeit von Programmen reduziert werden.
- Um dies zu ermöglichen gibt es zwei Varianten:
- parallele Prozesse
- parallele Threads
Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Prozesse VS Threads
- Parallele Prozesse:
- Laufen in einem anderen Kontext
- Keinen Zugriff auf Variablen von anderen Prozessen
- Parallele Threads:
- Laufen im selben Kontext
- Können auf Variablen von anderen Threads im selben Kontext zugreifen
- Schnelleres Task-Switching
- Daten können geteilt werden
- Kann aber zu Problemen in der Synchronisation geben, wenn man Daten mit anderen Threads teilt
Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Multithreading
- Mit ".start()" Kann man einen Thread starten. Dieser wird dann im Hintergrund ausgeführt, das heisst es wird nicht gewartet bis die Funktion fertig ist, sondern das Programm geht direkt weiter.
- Die "run" Funktion vom Thread wird ausgeführt wenn ".start()" aufgerufen wird.
k: 4‘000‘000, j: 3‘752‘884 k: 4‘000‘000, j: 10‘806‘936 k: 4‘000‘000, j: 7‘307‘897 k: 4‘000‘000, j: 5‘322‘116 k: 4‘000‘000, j: 4‘366‘084
public class Worker extends Thread {
static int j = 0;
int k = 0;
@Override
public void run() {
for (int i = 0; i < 4000000; i++) {
j++;
k++;
}
System.out.println("k: " + k + " j:" + j);
}
} public class Main {
public static void main(String[] args) {
for (int i = 0; i < 5; i++){
new Worker().start();
}
}
}Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Multithreading
k: 4‘000‘000, j: 3‘752‘884 k: 4‘000‘000, j: 10‘806‘936 k: 4‘000‘000, j: 7‘307‘897 k: 4‘000‘000, j: 5‘322‘116 k: 4‘000‘000, j: 4‘366‘084
- Warum hat j nie 20'000'000 erreicht?
- Wenn mehrere Threads gleichzeitig j++ aufrufen kann es sein, dass j nachher noch denselben Wert hat.
- Das Problem kommt daher, dass die Threads gleichzeitig den selben alten Wert von j lesen, jeder ihn einzeln inkrementiert und dann alle ihren Wert wieder in j speichern.
- Danach ist j nur um 1 inkrementiert worden.
Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Multithreading
j = 7
Thread 1
Thread 2
7
+1
=8
=8
+1
7
1
2
3
4
5
6
- Thread 1 liest j aus dem Speicher
- Thread 1 fängt an j zu inkrementieren
- Während Thread 1 am inkrementieren ist, lädt Thread 2 j aus dem Speicher
- Thread 2 fängt an j zu inkrementieren
- Thread 1 ist fertig und speichert den neuen Wert
- Thread 2 ist fertig und überschreibt den Wert von Thread 1 nochmals mit dem selben Wert
j = 8
Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Multithreading
k: 4‘000‘000, j: 3‘752‘884 k: 4‘000‘000, j: 10‘806‘936 k: 4‘000‘000, j: 7‘307‘897 k: 4‘000‘000, j: 5‘322‘116 k: 4‘000‘000, j: 4‘366‘084
- Warum sind die Outputs nicht aufsteigend sortiert?
- Der Wert von j wächst stetig, er wird nicht wieder kleiner
- Die System.out.println funktion ist jedoch nicht verlässlich, wenn sie gleichzeitig von mehreren Threads aufgerufen wird.
- Der Output muss also nicht zwingend in der Reihenfolge sein in welcher System.out.println aufgerufen wurde.
Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Multithreading
- Mit "synchronized" kann man gewisse Programmabschnitte synchronisieren
- Man braucht ein geteiltes Objekt (hier "lock") als Schloss
- Es kann immer nur ein Thread gleichzeitig im synchronisierten Bereich sein.
k: 4‘000‘000, j: 15‘786‘100 k: 4‘000‘000, j: 18‘432‘690 k: 4‘000‘000, j: 19‘408‘717 k: 4‘000‘000, j: 19‘344‘207 k: 4‘000‘000, j: 20‘000‘000
public class Worker extends Thread {
static int j = 0;
int k = 0;
static Object lock = new Object();
@Override
public void run() {
for (int i = 0; i < 4000000; i++) {
synchronized(lock){
j++;
}
k++;
}
System.out.println("k: " + k + " j:" + j);
}
} public class Main {
public static void main(String[] args) {
for (int i = 0; i < 5; i++){
new Worker().start();
}
}
}Pascal Schärli - PVK Informatik II 2021
Parallele Programmierung
Multithreading
- Mit "join" kann man warten bis ein Thread fertig ist.
- So ist es mehrere Threads zu starten und dann zu warten bis alle fertig sind.
- Es kann immer nur ein Thread gleichzeitig im synchronisierten Bereich sein.
k: 4‘000‘000, j: 15‘786‘100 k: 4‘000‘000, j: 18‘432‘690 k: 4‘000‘000, j: 19‘344‘207 k: 4‘000‘000, j: 19‘408‘717 k: 4‘000‘000, j: 20‘000‘000 Done!
public static void main(String[] args) {
Worker workers[] = new Worker[5];
for (int i = 0; i < 5; i++) {
workers[i] = new Worker();
workers[i].start();
}
for (int i = 0; i < 5; i++) {
try {
workers[i].join();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
System.out.println("Done!");
}Pascal Schärli - PVK Informatik II 2021
Frühling 2018, 0.75 Notenpunkte
Parallelität
Prüfungsaufgabe
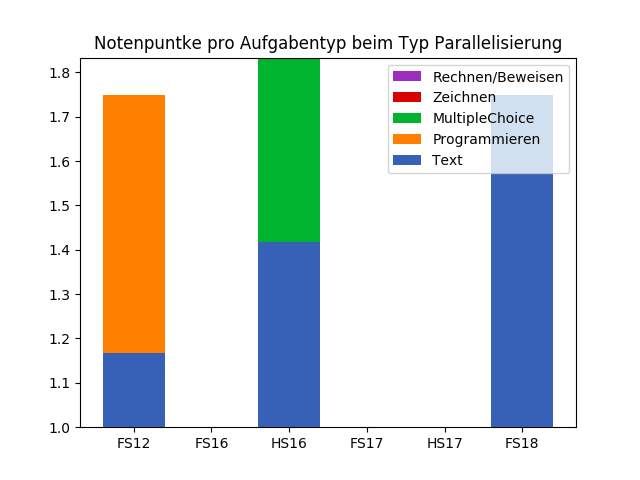
Pascal Schärli - PVK Informatik II 2021
Parallelität
Prüfungsaufgabe
Frühling 2018, 0.75 Notenpunkte
public class ParIncr extends Thread {
int i; // individuelle Variable
static int j; // gemeinsame Var.
static Object Sperre = new Object();
public void run() {
for (i = 0; i < 400000000; i++) {//400'000'000
synchronized (Sperre) {
j++;
}
}
System.out.println("i: " + i + " j: " + j);
}
public static void main(String[] args) {
ParIncr[] workers = new ParIncr[5];
for (int k = 0; k < 5; k++) {
workers[k] = new ParIncr();
workers[k].start();
}
for (int k = 0; k < 5; k++) {
try {
workers[k].join();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}- Höchste Ausgabe für j:
- 2'000'000'000
- Ohne Sperre:
- i bleibt gleich, aber j würde die 2'000'000'000 nicht erreichen.
- "Sperre" mit "this ersetzen:
- "this" ist für jeden Thread ein anderes Objekt, somit können die Threads trotz synchronized gleichzeitig auf j zugreifen.
Pascal Schärli - PVK Informatik II 2021
Parallelität
Prüfungsaufgabe
Frühling 2018, 0.75 Notenpunkte
public class ParIncr extends Thread {
int i; // individuelle Variable
static int j; // gemeinsame Var.
static Object Sperre = new Object();
public void run() {
for (i = 0; i < 400000000; i++) {//400'000'000
synchronized (Sperre) {
j++;
}
}
System.out.println("i: " + i + " j: " + j);
}
public static void main(String[] args) {
ParIncr[] workers = new ParIncr[5];
for (int k = 0; k < 5; k++) {
workers[k] = new ParIncr();
workers[k].start();
}
for (int k = 0; k < 5; k++) {
try {
workers[k].join();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}- "static" bei "Sperre" weglassen:
- Da nun "Sperre" für jeden Thread ein anderes Objekt ist, können die Threads trotz synchronized gleichzeitig auf j zugreifen.
- Durch das Lock können die extra Prozessoren nicht parallel genutzt werden und es gibt einen Overhead beim Wechsel zwischen den einzelnen Threads.
Pascal Schärli - PVK Informatik II 2021
Programmverifikation

Pascal Schärli - PVK Informatik II 2021
Schleifeninvarianten
Programmverifikation
Schleifen Körper
Schleife
- Die Schleifeninvariante hat nach dem Schleifenkörper wieder den selben Wert, den sie vor dem Schleifenkörper gehabt hat.
- Falls man zeigen kann, dass die Invariante vor der Schleife gilt, so gilt sie auch nach der Schleife.
Definition:
Schleifeninvarianten sind ein Weg um die Korrektheit einer Funktion zu beweisen.
static int f(int i, int j) {
assert(i >= 0 && j >= 0);
int u = i;
int z = 0;
// [Vor Schleife]
while (u > 0){
// [Vor Schleifenkörper]
z = z + j;
u = u - 1;
// [Nach Schleifenkörper]
}
// [Nach Schleife]
return z;
}Pascal Schärli - PVK Informatik II 2021
1. Beweise, dass dies eine korrekte Scheifeninvariante ist:
\(z + u * j − i * j = 0 \text{ und }u \geq 0\)
static int f(int i, int j) {
assert(i >= 0 && j >= 0);
int u = i;
int z = 0;
// [Vor Schleife]
while (u > 0){
// [Vor Schleifenkörper]
z = z + j;
u = u - 1;
// [Nach Schleifenkörper]
}
// [Nach Schleife]
return z;
}- Vor Schleifenkörper
-
\(z_n + u_n * j - i * j = 0\)
- \(u_n > 0\)
-
- Nach Schleifenkörper
\(z_{n+1} = z_n + j\)
\(u_{n+1} = u_n - 1\)- \(z_{n+1} + u_{n+1}* j - i*j\)
\(= z_n + j + (u_n-1)*j - i*j = z_n + u_n *j - i*j = 0 \)
\(\Rightarrow z_{n+1} + u_{n+1}* j - i*j = 0\) - \(u_{n+1} = u_n - 1 > -1\)
\(\Rightarrow u_{n+1} \geq 0\)
- \(z_{n+1} + u_{n+1}* j - i*j\)
(Schleifeninvariante)
(Sonst wären wir nicht in den while-loop gekommen)
\(\Rightarrow\) Schleifeninvariante gilt auch nach Schleifenkörper
Programmverifikation
Schleifeninvarianten
Pascal Schärli - PVK Informatik II 2021
2. Zeige, dass die Schleifeninvariante vor der Schleife gilt
\(z + u * j − i * j = 0 \text{ und }u \geq 0\)
static int f(int i, int j) {
assert(i >= 0 && j >= 0);
int u = i;
int z = 0;
// [Vor Schleife]
while (u > 0){
// [Vor Schleifenkörper]
z = z + j;
u = u - 1;
// [Nach Schleifenkörper]
}
// [Nach Schleife]
return z;
}-
\(z + u * j − i * j = 0\)
\(0 + i * j − i * j = 0\)
\(0 = 0\) ✓ -
u >= 0
i >= 0 ✓
1.
2.
Schleifeninvarianten
Programmverifikation
Pascal Schärli - PVK Informatik II 2021
static int f(int i, int j) {
assert(i >= 0 && j >= 0);
int u = i;
int z = 0;
// [Vor Schleife]
while (u > 0){
// [Vor Schleifenkörper]
z = z + j;
u = u - 1;
// [Nach Schleifenkörper]
}
// [Nach Schleife]
return z;
}-
\(z + u * j − i * j = 0\)
\(u \geq 0\) -
\(u \leq 0\)
Daraus folgt:
-
\(0 \leq u \leq 0 \Rightarrow u = 0\)
-
\(z + 0*j - i*j = 0\)
\(\Rightarrow z = i * j\)
(Schleifeninvariante)
(Sonst wären wir nicht aus dem while-loop gekommen)
Schleifeninvarianten
Programmverifikation
\(z + u * j − i * j = 0 \text{ und }u \geq 0\)
3. Daraus folgt, dass sie auch nach der Schleife gilt.
Pascal Schärli - PVK Informatik II 2021
Schleifeninvarianten
Programmverifikation
Pascal Schärli - PVK Informatik II 2021
Wie findet man eine Schleifeninvariante?
- Es gibt keinen Weg eine Schleifeninvariante zu finden, welche den gewünschten Beweis ermöglicht.
- Es ist nur möglich zu prüfen ob eine Gegebene Invariante funktioniert.
- Probiert eine Invariante aus, schaut ob der Beweis funktioniert.
- Es mir hilft zu schauen, was ich nach der Schleife zeigen will und was vor der Schleife gilt.
Herbst 2017, 0.58 Notenpunkte
Programmverifikation
Prüfungsaufgabe
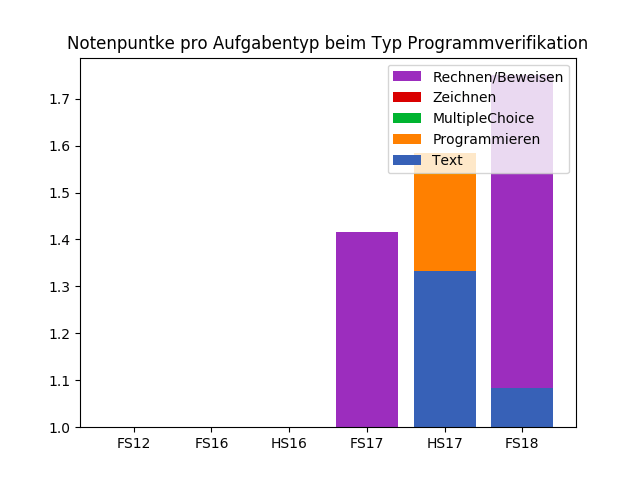
Pascal Schärli - PVK Informatik II 2021
Programmverifikation
Prüfungsaufgabe
Herbst 2017, 0.58 Notenpunkte
public static int mult(int i, int j) {
int a = i;
int b = j;
int z = 0;
while(b > 0) {
if(b%2 != 0) {
z = z + a;
b = b - 1;
}
b = b / 2;
a = 2 * a;
}
return z;
}public static int power(int i, int j) {
int a = i;
int b = j;
int z = 1;
while(b > 0) {
if(b%2 != 0) {
z = z * a;
b = b - 1;
}
b = b / 2;
a = a * a;
}
return z;
}Pascal Schärli - PVK Informatik II 2021
Programmverifikation
Prüfungsaufgabe
Herbst 2017, 0.58 Notenpunkte
- Theorietisch wäre hier jede Schleifeninvariante akzeptiert, also auch "z = z"
- Es muss einfach folgendes gelten:
Falls die Invariante vor dem Schleifenkörper gilt, so muss sie auch nach dem Schleifenkörper gelten - Eine Invariante, mit welcher der Beweis nachher funktioniert wäre
\(z \cdot a^b = i^j\)
Pascal Schärli - PVK Informatik II 2021
Programmverifikation
Prüfungsaufgabe
Herbst 2017, 0.58 Notenpunkte
Schleifeninvariante \(z \cdot a^b = i^j\)
- Fall 1: \(b \% 2 = 0\)
- \(z_{n+1} = z_{n}\)
- \(a_{n+1} = a_{n} ^ 2\)
- \(b_{n+1} = \frac{b_{n}}{2}\)
- \(z_{n+1} \cdot a_{n+1}^{b_{n+1}} = z_{n} \cdot a_{n} ^ {(2 \cdot \frac{b_n}{2})}\)
\(= z_n \cdot a_n ^ {b_n} = i^j\)
public static int power(int i, int j) {
int a = i;
int b = j;
int z = 1;
while(b > 0) {
if(b%2 != 0) {
z = z * a;
b = b - 1;
}
b = b / 2;
a = a * a;
}
return z;
}Pascal Schärli - PVK Informatik II 2021
Programmverifikation
Prüfungsaufgabe
Herbst 2017, 0.58 Notenpunkte
Schleifeninvariante \(z \cdot a^b = i^j\)
- Fall 2: \(b \% 2 \neq 0\)
- \(z_{n+1} = z_{n} * a_n\)
- \(a_{n+1} = a_{n} ^ 2\)
- \(b_{n+1} = \frac{b_{n} - 1}{2}\)
- \(z_{n+1} \cdot a_{n+1}^{b_{n+1}} = z_{n} \cdot a_n \cdot a_{n} ^ {(2 \cdot \frac{(b_n - 1)}{2})}\)
\(= z_n \cdot a_n ^ {b_n} = i^j\)
public static int power(int i, int j) {
int a = i;
int b = j;
int z = 1;
while(b > 0) {
if(b%2 != 0) {
z = z * a;
b = b - 1;
}
b = b / 2;
a = a * a;
}
return z;
}\(\Rightarrow\) somit haben wir in beiden Fällen gezeigt, dass falls die Schleifeninvariante vor dem Schleifenkörper gilt, sie auch nach dem Schleifenkörper gelten muss.
Pascal Schärli - PVK Informatik II 2021
Programmverifikation
Prüfungsaufgabe
Herbst 2017, 0.58 Notenpunkte
- Jetzt müssen wir zeigen, dass die Invariante vor der Schleife gilt:
- \(a = i\)
- \(b = j\)
- \(z = 1\)
- \(z \cdot a^b = i^j\)
- \(1 \cdot i^j = i^j\)
- Somit gilt sie auch nach der Schleife
public static int power(int i, int j) {
int a = i;
int b = j;
int z = 1;
while(b > 0) {
if(b%2 != 0) {
z = z * a;
b = b - 1;
}
b = b / 2;
a = a * a;
}
return z;
}Pascal Schärli - PVK Informatik II 2021
Programmverifikation
Prüfungsaufgabe
Herbst 2017, 0.58 Notenpunkte
- Nach der Schleife gilt also die Schleifeninvariante immernoch: \(z \cdot a^b = i^j\)
- Zusätzlich wissen, wir dass die Schleife abgebrochen hat, daher wissen wir, dass \(b = 0\)
- Zusammen ergibt sich
\(z \cdot a^0 = z = i^j\)
public static int power(int i, int j) {
int a = i;
int b = j;
int z = 1;
while(b > 0) {
if(b%2 != 0) {
z = z * a;
b = b - 1;
}
b = b / 2;
a = a * a;
}
return z;
}Pascal Schärli - PVK Informatik II 2021
Spieltheorie

Pascal Schärli - PVK Informatik II 2021
Spielbäume
Spieltheorie
Grün
gewinnt
Grün
gewinnt
Grün
gewinnt
Blau
gewinnt
Blau
gewinnt
Spielregeln:
- Die Spieler können abwechslungsweise entweder 1 oder 2 Zündhölzer ziehen.
- Der Spieler, welcher das letzte Zündholz nimmt hat verloren.














Pascal Schärli - PVK Informatik II 2021














Spielregeln:
- Die Spieler können abwechslungsweise entweder 1 oder 2 Zündhölzer ziehen.
- Der Spieler, welcher das letzte Zündholz nimmt hat verloren.
Blau
gewinnt
Blau
gewinnt
Grün
gewinnt
Grün
gewinnt
Grün
gewinnt
Blau
gewinnt
Blau
gewinnt
Grün
gewinnt
Grün
gewinnt
Grün
gewinnt
Grün
gewinnt
Grün
gewinnt
\(\Rightarrow\) Grün gewinnt!
Pascal Schärli - PVK Informatik II 2021
Spielbäume
Spieltheorie
Und-Oder Baum
Spieltheorie
- Wenn man beim Minimax-Algorithmus nur binäre Werte hat, kann man den Baum auch als Und-Oder Baum verstehen.
- Min-Knoten werden zu einem logischen AND
- Max-Knoten werden zu einem logischen OR
0
0
0
1
1
AND
AND
AND
OR
OR
OR
OR
1
1
0
0
0
0
0
\(\Rightarrow\) Blau verliert!
Pascal Schärli - PVK Informatik II 2021
Minimax
Spieltheorie
- Der Minimax Algorithmus führt dieselben Überlegungen wie im Zündholz-Beispiel aus.
- Wir haben zwei Spieler, der Min-Spieler möchte den Wert der Wurzel minimieren und der Max-Spieler möchte ihn Maximieren.
- Ein Min-Knoten nimmt daher das Minimum der Werte von seinen Kindern als sein eigener Wert.
- Umgekehrt nimmt der Max-Knoten das Maximum der Werte von seinen Kindern als sein eigener Wert.
Pascal Schärli - PVK Informatik II 2021
6
6
2
9
8
9
5
2
7
9
5
3
4
6
7
3
7
Max
Max
Min
Min
Minimax
Spieltheorie
Pascal Schärli - PVK Informatik II 2021
6
9
\(\geq\)9
\(\leq\)6
Max
Min
Min
\([\ldots]\)
Da Min den Wert aller Kinder minimiert, muss dieser Knoten \(\leq 6\) sein
Da Max den Wert aller Kinder maximiert, muss dieser Knoten \(\geq 9\) sein
Da Min sowieso den Weg A wählen wird, müssen wir den Wert der restlichen Knoten nicht mehr auswerten
Weg A
Weg B
Alpha Beta
Spieltheorie
Pascal Schärli - PVK Informatik II 2021
- Jeder Knoten hat zwei Einschränkungen:
- \(\alpha\): Mindestwert, wecher Max sicher erreichen kann
- \(\beta\): Maximalwert, welcher Min höchstens einstecken muss
- Das Intervall \([\alpha, \beta]\) beinhaltet alle möglichen Werten für einen Knoten, mit welchen dieser für die Auswertung relevant wäre
- Falls \(\alpha \geq \beta \Rightarrow\) Cut
- Wenn der \(\alpha\) Wert den \(\beta\) Wert überschreitet muss man den Knoten nicht mehr weiter auswerten, da dieser Weg sowieso nicht gewählt werden wird.
- Wir notieren die Werte mit \([\alpha, \beta]\) bei den Kanten, welche vom Knoten wegführen.
- Schnitte nach dem Min-Knoten nennt man \(\alpha\)-Schnitte,
Schnitte nach dem Max-Knoten nennt man \(\beta\)-Schnitte.
Alpha Beta
Spieltheorie
Pascal Schärli - PVK Informatik II 2021
6
9
9
6
Max
Min
Min
\([- \infty, \infty]\)
Am Anfang gibt es noch keine Einschränkungen
\(\alpha = -\infty, \beta = \infty\)
Jetzt wissen wir, dass der Wert \(\leq 6\) ist.
\(\beta = 6\)
\([- \infty, 6]\)
\([- \infty, 6]\)
\([9, 6]\)
Wir wissen, der blaue Knoten hat einen Wert \(\geq 9\), daher gilt
\(\alpha = 9\)
Da \(\alpha \geq \beta\) müssen wir nicht mehr weiterrechnen
Alpha Beta
Spieltheorie
Pascal Schärli - PVK Informatik II 2021
6
6
2
9
8
9
5
2
7
\(\geq\)8
5
3
4
6
7
\(\leq\)5
7
Max
Max
Min
Min
\([- \infty, \infty]\)
\([- \infty, \infty]\)
\([- \infty, \infty]\)
\([6, \infty]\)
\([-\infty, 6]\)
\([6, \infty]\)
\([6, \infty]\)
\([6, \infty]\)
\([6, \infty]\)
\([6, 5]\)
\([6, \infty]\)
\([6, 7]\)
\([6, 7]\)
\([8, 7]\)
\([6, \infty]\)
Alpha Beta
Spieltheorie
Pascal Schärli - PVK Informatik II 2021
- Es gibt ein cooles Alpha-Beta Übungstool, es ist nicht von mir aber ich hoste es auf meiner Webseite:
https://pascscha.ch/info2/abTreePractice/
- Dort könnt ihr beliebig viele Alpha-Beta Beispiele lösen haben, oder selber lösen und korrigieren lassen.
- Aufpassen: Bei diesem Beispiel werden die Alpha-Beta Schranken neben den Knoten gezeigt und laufend aktualisiert. Wir haben bei uns die Konvention die Schranken unter dem Knoten bei den ausgehenden Kanten zu schreiben.
Pascal Schärli - PVK Informatik II 2021
Frühling 2016, 0.58 Notenpunkte
Bäume
Prüfungsaufgabe
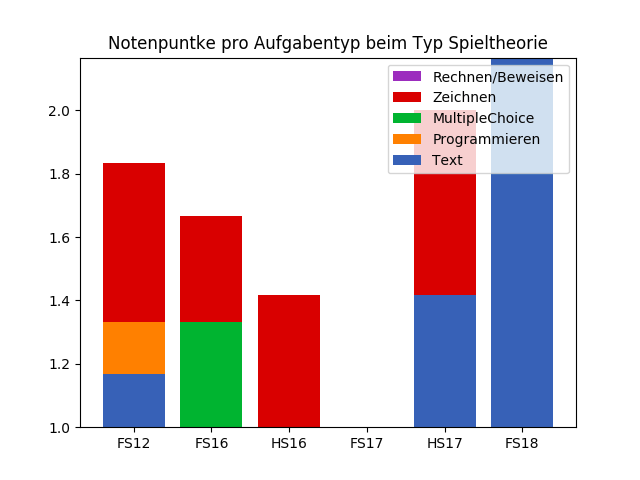
Pascal Schärli - PVK Informatik II 2021
Bäume
Prüfungsaufgabe
Frühling 2016, 0.58 Notenpunkte
Min
Min
Max
Max
4
2
1
4
3
5
2
9
1
3
5
3
1
4
4
3
8
Pascal Schärli - PVK Informatik II 2021
Bäume
Prüfungsaufgabe
Frühling 2016, 0.58 Notenpunkte
Pascal Schärli - PVK Informatik II 2021
4
\(\leq 2\)
\(\leq 1\)
4
2
4
4
3
8
Min
Min
Max
Max
1
Bäume
Prüfungsaufgabe
Frühling 2016, 0.58 Notenpunkte
- Der Alpha-Beta-Algorithmus und der Minimax-Algorithmus liefern immer den selben Gewinnwert der Wurzel.
-
wahr - Alpha-Beta schneidet nur Äste ab, welche für den Wert der Wurzel irrelevant sind.
-
wahr - Alpha-Beta schneidet nur Äste ab, welche für den Wert der Wurzel irrelevant sind.
- Der Parameter α des Alpha-Beta-Algorithmus ist eine obere Schranke für den Gewinnwert des MAX-Spielers.
- falsch - Es ist eine untere Schranke
Pascal Schärli - PVK Informatik II 2021
Bäume
Prüfungsaufgabe
Frühling 2016, 0.58 Notenpunkte
- Der Parameter β des Alpha-Beta-Algorithmus kann zum Wegfall von tiefer liegenden Zügen des MAX-Spielers führen.
-
wahr - Unter einem cut können immer sowohl MIN als auch MAX Knoten sein.
-
wahr - Unter einem cut können immer sowohl MIN als auch MAX Knoten sein.
- Die Evaluationsreihenfolge kann einen wesentlichen Einfluss auf die Geschwindigkeit des Alpha-Beta-Algorithmus haben.
- wahr - Wenn die besten Knoten am Anfang ausgewertet werden hat man früher ein engeres Alpha-Beta Intervall und kann somit mehr Schnitte machen.
Pascal Schärli - PVK Informatik II 2021
Simulationstechnik

Pascal Schärli - PVK Informatik II 2021
Motivation
Simulationstechnik
- Mit Hilfe der Simulationstechnik können Modelle von komplexen Prozessen simuliert werden.
- Dies erlaubt uns und vorhersagen über die Entwicklung des Prozesses in der realen Welt zu machen.
- Es gibt immer einen Zustand, welcher nach den Regelnd von unserem Modell verändert wird.
- Wir kennen zwei Methoden wann wir diese Regeln auf unser Modell anwenden:
- Zeitgesteuerte Simuation
- Ereignisgesteuerte Simulation
Pascal Schärli - PVK Informatik II 2021
Zeitgesteuerte Simulation
Simulationstechnik
- Der Zustand wird regelmässig immer jeden Zeitschritt \(\Delta t\) aktualisert.
- Mit \(\Delta t\) kann man die "Auflösung" der Simulation bestimmen. Kleiner \(\Delta t\) führen zu genaueren Werten aber auch zu mehr Rechenaufwand.
- Ein Beispiel dafür wäre zum Beispiel die Simulation von einem schiefen Wurf
Pascal Schärli - PVK Informatik II 2021
Zeitgesteuerte Simulation
Simulationstechnik
class Ball{
double posX, posY, velX, velY;
final static double g = 9;
public Ball(double posX, double posY, double velX, double velY) {
this.posX = posX;
this.posY = posY;
this.velX = velX;
this.velY = velY;
}
public void update(double dt) {
velY -= g * dt;
posX += velX * dt;
posY += velY * dt;
}
}Ball ball = new Ball(0,0,10,20);
double dt = 1;
for(int i = 0; i < 5; i++) {
System.out.println("x:"+ball.posX+" y:"+ball.posY);
ball.update(dt);
}Zustand
Aktualisierung um \(\Delta t\)
x:0.0 y:0.0
x:10.0 y:11.0
x:20.0 y:13.0
x:30.0 y:6.0
x:40.0 y:-10.0Pascal Schärli - PVK Informatik II 2021
Ereignisgesteuerte Simulation
Simulationstechnik
- Der Zustand bleibt abschnittweise konstant und wird immer nur nach gewissen Ereignissen aktualisiert.
- Die Zeit steigt dabei nicht konstant an sondern wächst sprunghaft.
- Ein Beispiel dafür wäre zum Beispiel ein Promillerechner.
Pascal Schärli - PVK Informatik II 2021
Ereignisgesteuerte Simulation
Simulationstechnik
0.3571428571428572
4.642857042857144Zustand zu beliebiger Zeit aktualisieren
Zustand
Promille p = new Promille();
p.addDrink(0.5, 0.05); // drink a beer
System.out.println(p.getPromille());
p.addDrink(0.75, 0.4); // drink a bottle of rum
System.out.println(p.getPromille());class Promille {
private double promille;
private long last_update;
final static double process_speed = 2. / 100000000;
final static double absorb_speed = 100. / 7;
public Promille() {
promille = 0;
last_update = System.currentTimeMillis();
}
public double getPromille() {
long now = System.currentTimeMillis();
double processed = (now - last_update) * process_speed;
promille = Math.max(0, promille - processed);
last_update = now;
return promille;
}
public void addDrink(double amount, double strength) {
promille = getPromille() + amount * strength * absorb_speed;
}
}Pascal Schärli - PVK Informatik II 2021
That's it!
Pascal Schärli - PVK Informatik II 2021
- Am 19. Januar, 9:00 – 12:00 findet eine Zoom-Fragestunde statt.
- Der PVK wurde aufgenommen und wird euch zur Verfügung gestellt.
- Viel Erfolg, Spass und Ausdauer in der Lernphase und ich wünsche euch allen eine super Prüfung!
Viel Spass!
Pascal Schärli - PVK Informatik II 2021